正規分布
正規分布とはあらゆるデータ=測定値(身長・体重など)や測定誤差などに当てはまる最も一般的な分布を指す。
正規分布は確率を面積で表す確率密度関数として描かれる。

例えば、正規分布では「平均値-標準偏差~平均値+標準偏差=μ-σ~μ+σ」の面積が全体の68.26%であることから「平均値-標準偏差~平均値+標準偏差=μ-σ~μ+σ」の範囲にデータが収まる確率は68.26%だと言える。
正規分布の重要な性質①
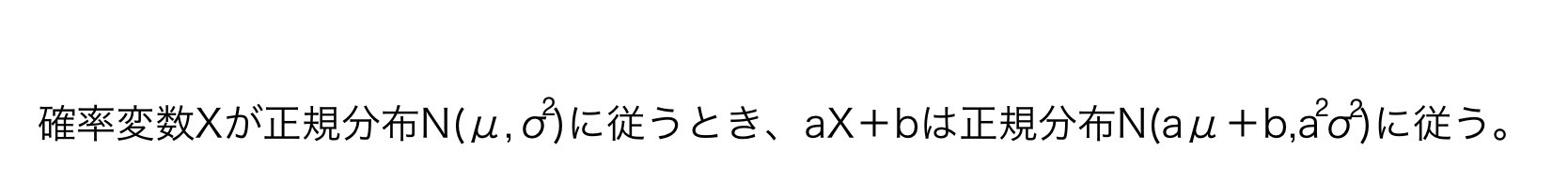
この性質を感覚的に理解する。
例X:{1,2,3,4,5,6,7,8,9,10}の分布
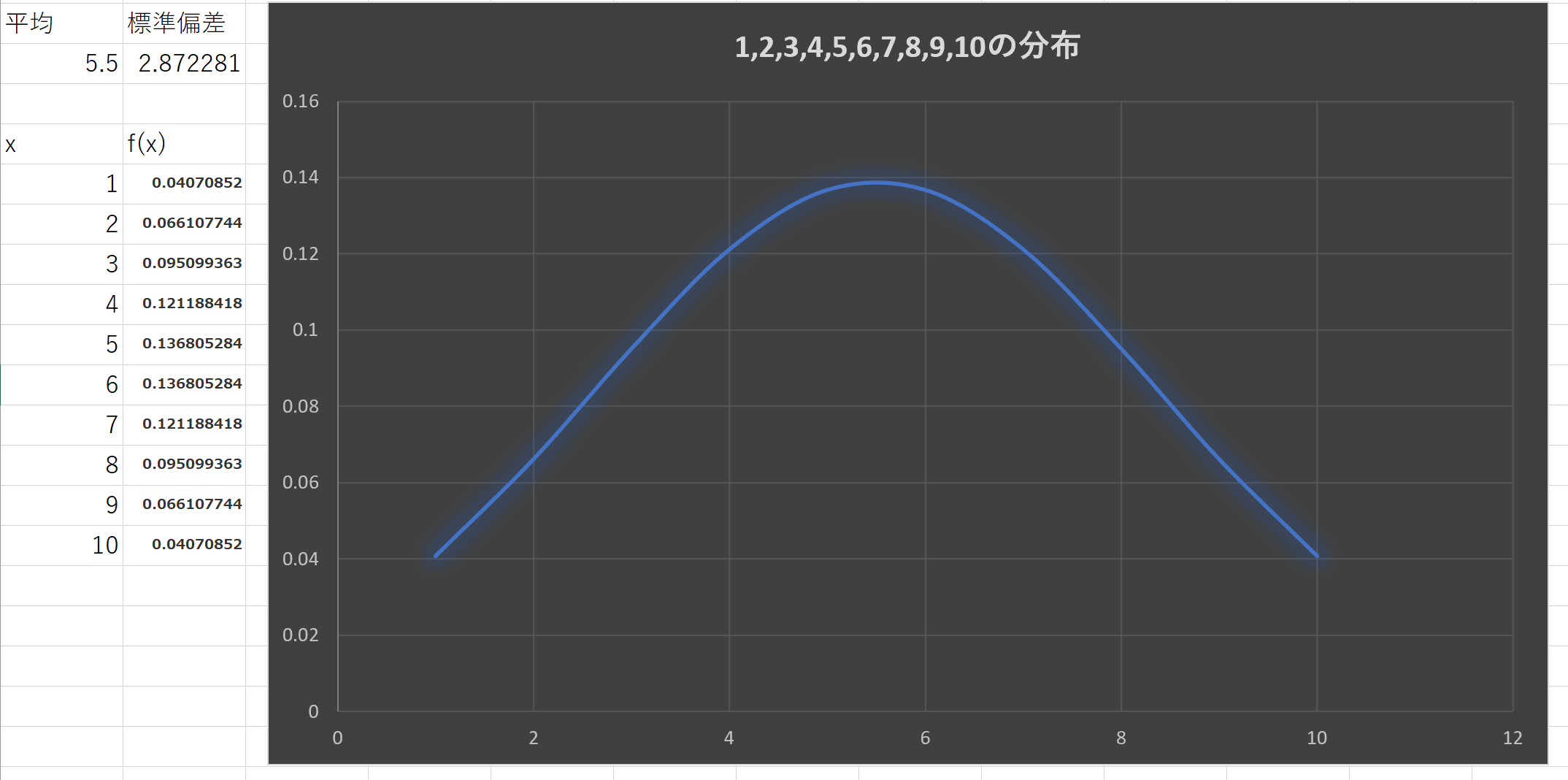
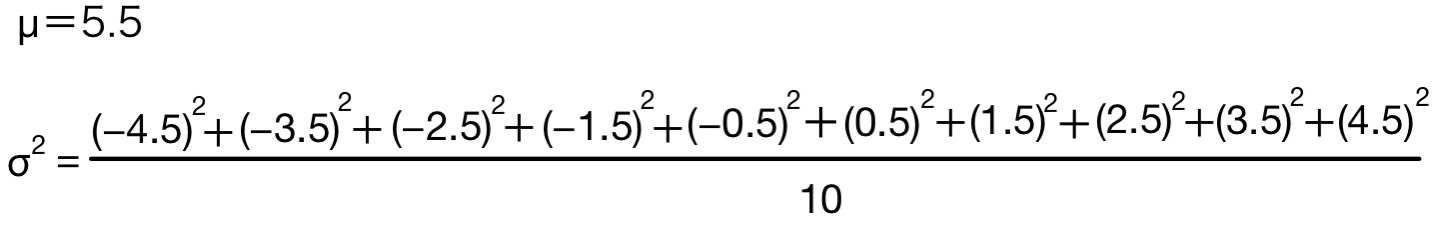
平均=5.5,分散=8.25,標準偏差=2.872281
これをa=1,b=0つまりXのときとする。
例2X:{2,4,6,8,10,12,14,16,18,20}の分布
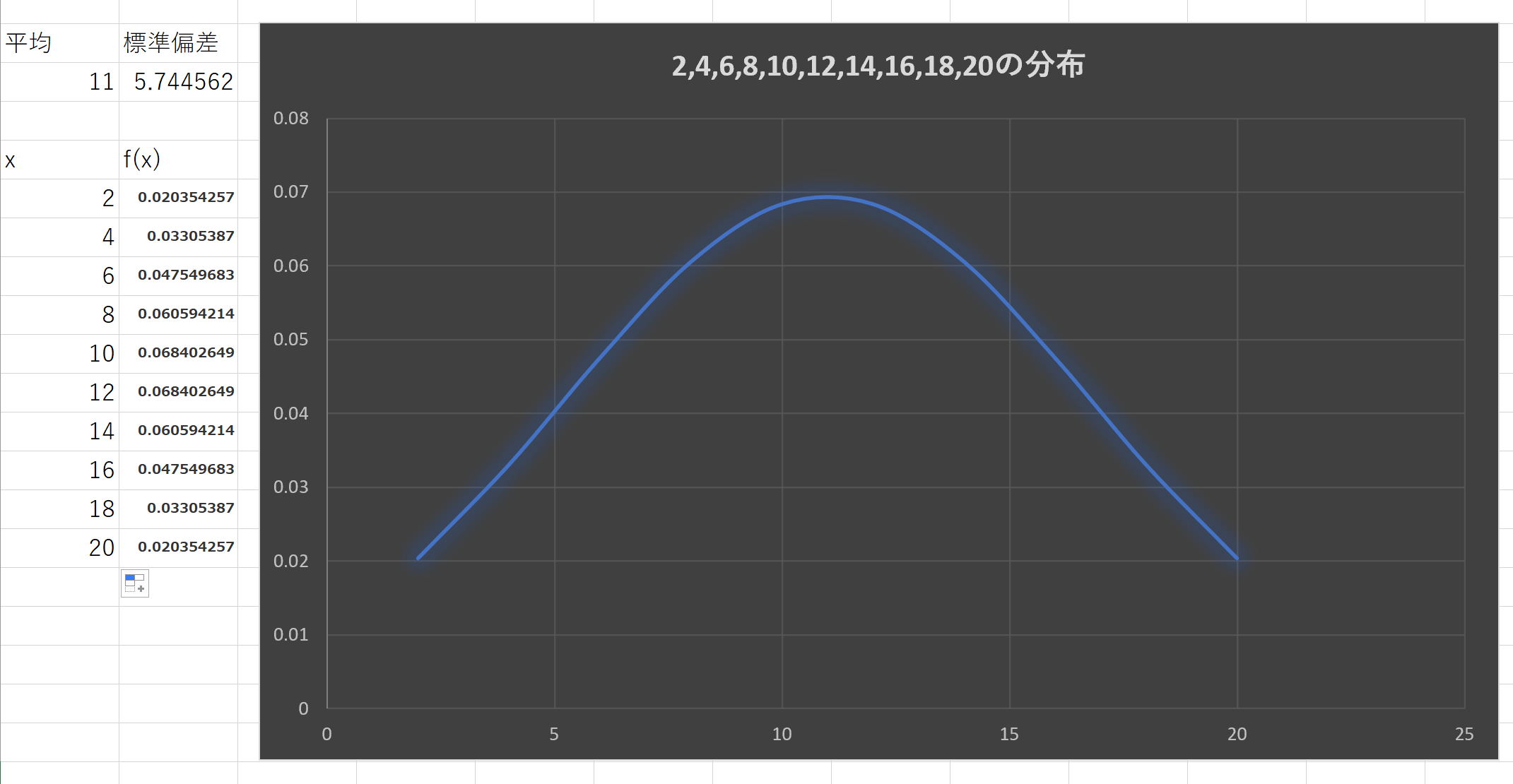
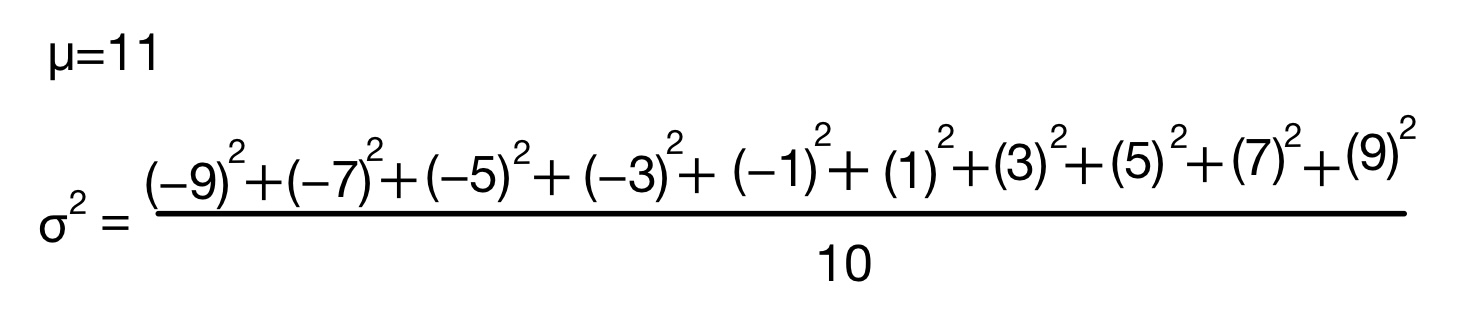
平均=11,分散=33,標準偏差=5.744562
これはa=2,b=0つまり2Xのときである。
例X+1:{2,3,4,5,6,7,8,9,10,11}の分布
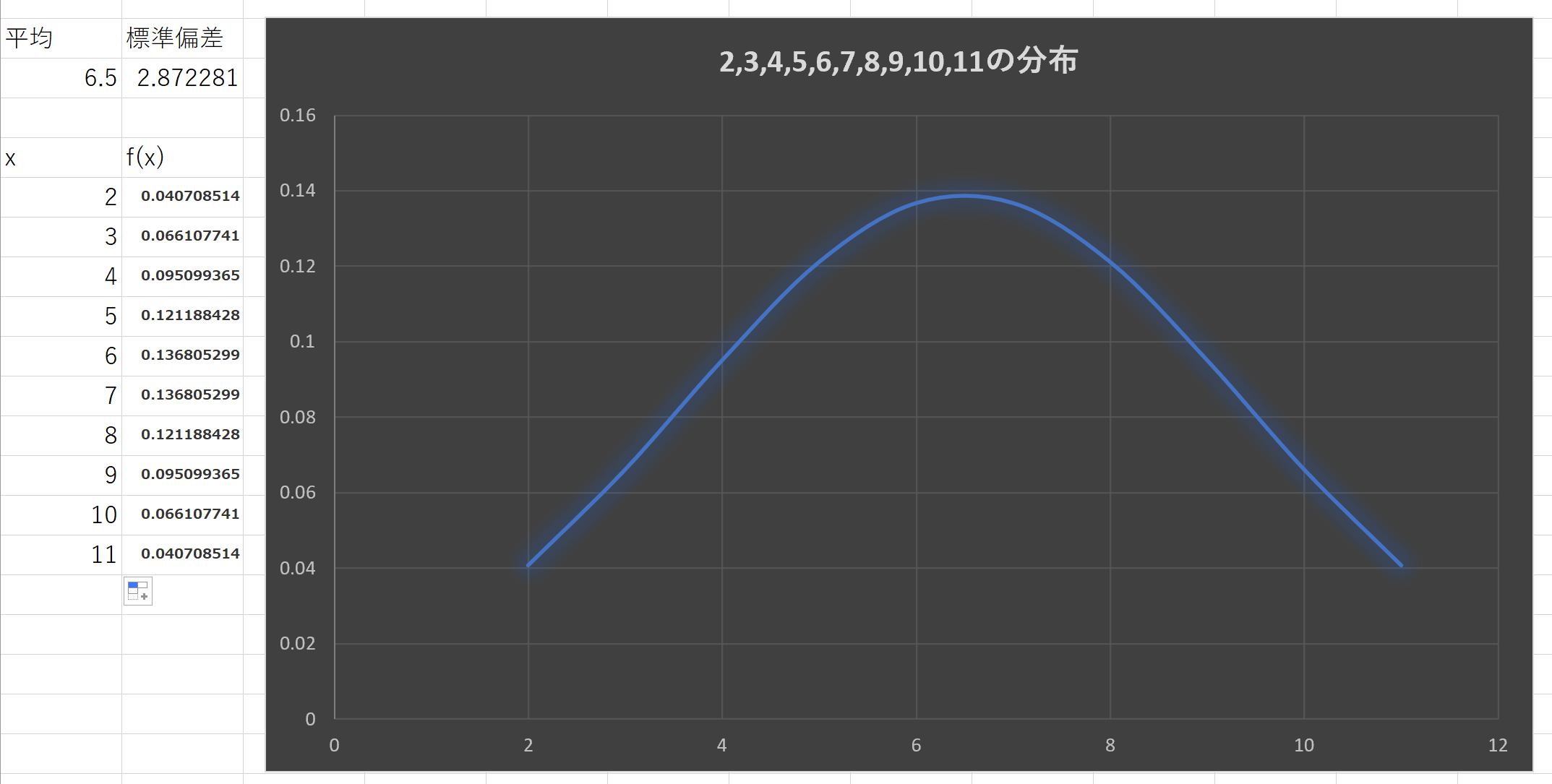
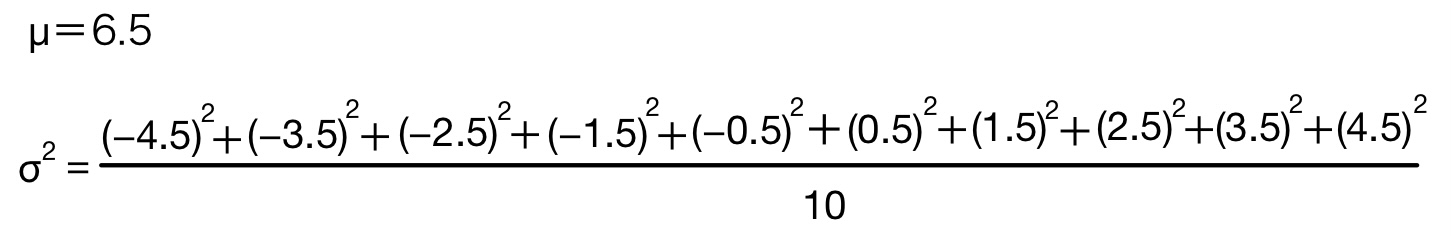
平均=6.5,分散=8.25,標準偏差=2.872281
これはa=1,b=1つまりX+1のときである。
例2X+1:{3,5,7,9,11,13,15,17,19,21}の分布
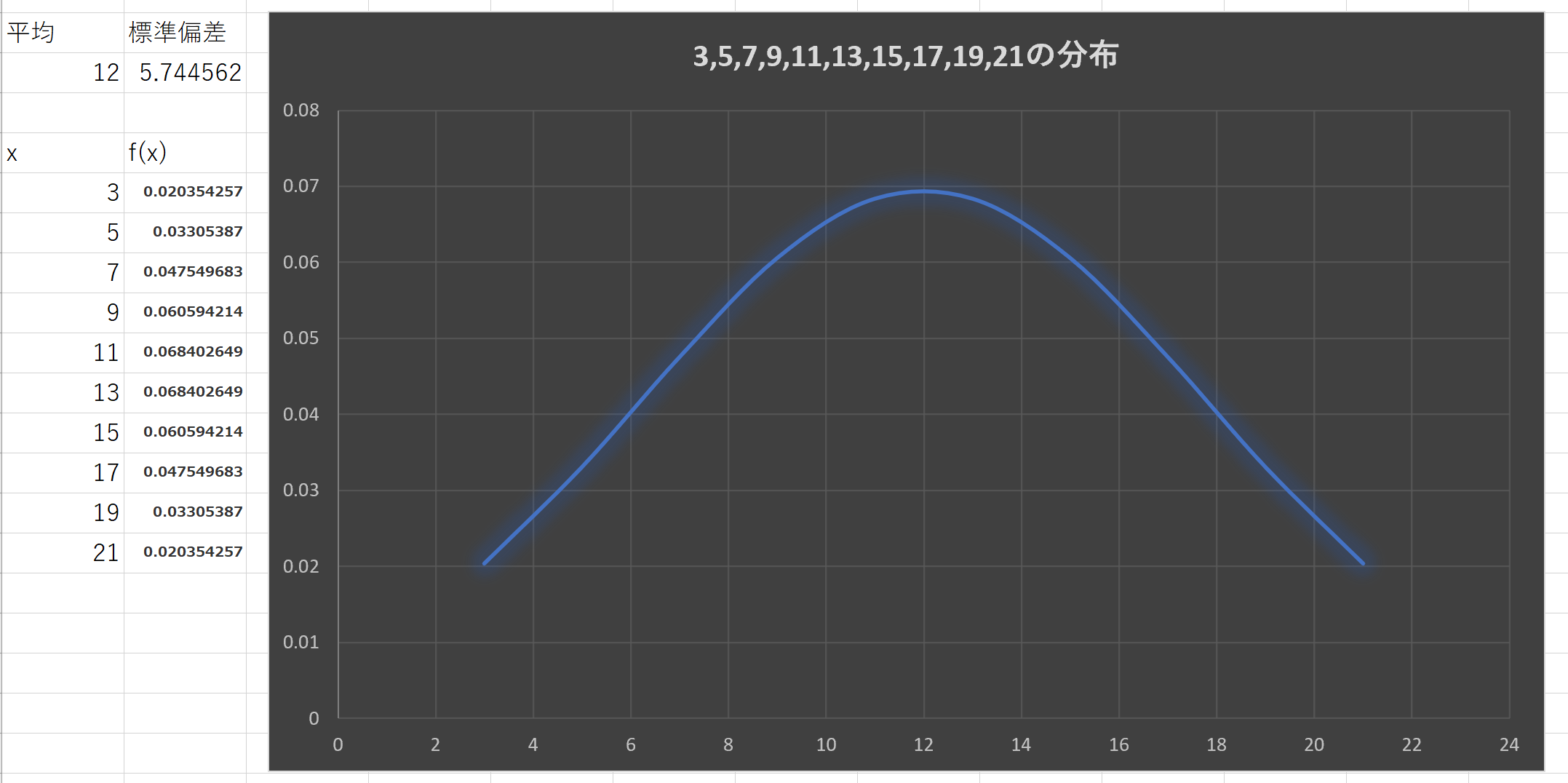
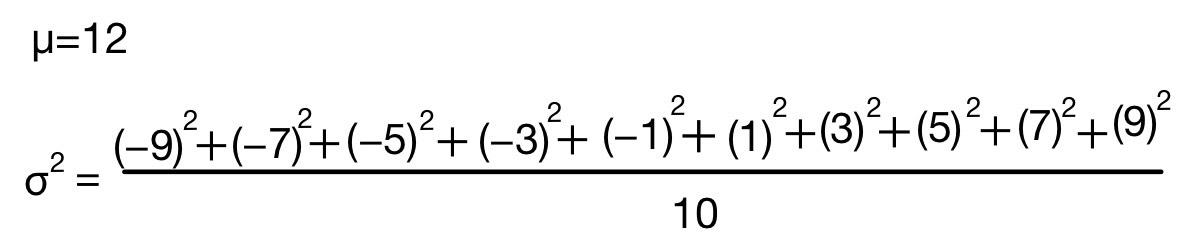
平均=12,分散=33,標準偏差=5.744562
これはこれはa=2,b=1つまり2X+1のときである。
標準正規分布への変換
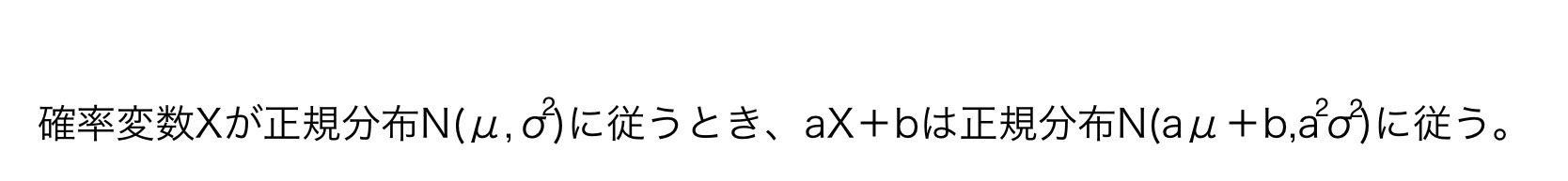
という正規分布の性質を用いて正規分布を標準正規分布に変換する。

通常、正規分布は標準正規分布に変換して「標準化」することでより使いやすくされる。
標準正規分布とは平均値が0で標準偏差が1の正規分布である。
Z値とは

標準正規分布には標準正規分布表があり、標準正規分布表を見れば「あるZ値以上が生じる確率」を求めることができる。また、正規分布左右対称であるので「あるZ値以上が生じる確率」と「あるZ値以下が生じる確率」が同じとなることから、「あるZ値以下が生じる確率」も知ることができる。

例えば、-1≦Z≦1となる確率は68.26%である。これは正規分布の「平均値-標準偏差~平均値+標準偏差=μ-σ~μ+σ」の範囲にデータが収まる確率は68.26%という性質でも分かることであり標準正規分布表を見るまでもない。
しかし、これが-1.1≦Z≦1.1となる確率を求めるとなると標準正規分布表を見て求めなければいけないことになる。標準正規分布表から「Z値が1.1以上となる確率=Z値が1.1以下となる確率」を求めてそれらを引けば「-1.1≦Z≦1.1となる確率」が分かる。
正規分布を標準正規分布にする理由はここにある。あらゆる正規分布一つ一つに正規分布表を作ることは面倒というか無理であるので、正規分布はいったん標準正規分布に変換して標準正規分布表で評価しようということになるのである。
ある正規分布でX値以上が生じる確率を求めたいときは、それに対応する標準正規分布を考えてZ値以上が生じる確率を標準正規分布表で探せば良い。
正規分布の重要な性質②(正規分布の再現性)

この性質を正規分布の再現性という。
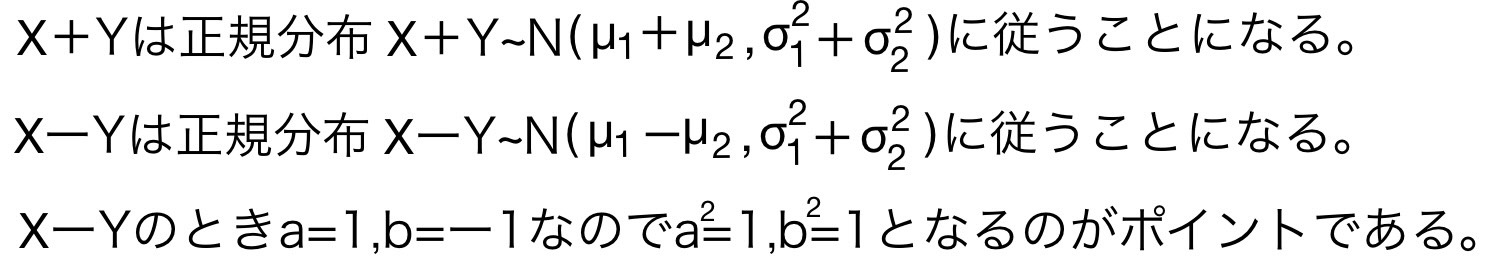
正規分布の再現性を具体例で考えてみる。
中心極限定理

中心極限定理は分かりにくいので具体例で考える。
中心極限定理によると、この100組の標本データ一つ一つの平均を算出して、その標本データごとの平均の分布(標本分布)を調べると正規分布N(60kg,0.06kg)に近づくことになる。
つまり、母集団から標本をたくさん作ってそれぞれ標本データごとの平均値(標本データ平均)を算出すると、標本データごとの平均値(標本データ平均)は正規分布に従う。そして、その標本データごとの平均値の平均値(標本データ平均の平均)は母平均と同じになり、標本データごとの平均値(標本データ平均)は母分散をサンプルサイズで割った分散で分布するのである。標本データごとの平均値(標本データ平均)の標準偏差を標準誤差という。
例えば、ある大学の学生の総数が1000人のときにそのうち999人を無作為に選んで体重を計測するという実験を繰り返すと、その一つ一つの標本データごとの平均の平均(標本データ平均の平均)が母平均に近づくのは感覚的に分かる。また、その一つ一つの標本データごとの平均(標本データ平均)の正規分布における分散はものすごく小さいことになることも想像がつく。母分散をサンプルサイズで割ったものが標本データごとの平均の分散であるが、これはサンプルサイズを大きくすればするほど標本データごとの平均の分散は小さくなっていくことを示している。
不偏分散
母集団から標本を抽出するとき、しばしば母平均・母分散が不明ということがよくある。そもそも標本を抽出する理由は母集団の母平均・母分散を推定するためだからである。母集団の母平均・母分散が分かっていたらわざわざ標本を抽出して調べる必要はない。
例えばある一つ高校の高校生の身長の平均と分散を知りたいときはその高校の生徒を全数調査をして調べることはそんなに難しそうではないが、日本全国の高校生の身長の平均と分散を知りたいときに日本全国の高校生全員を全数調査することは不可能である。
そこで日本全国の高校生の身長の平均と分散を知りたいときは、標本を抽出してその標本の平均と標本の分散から母平均と母分散を推定することになるのである。

標本は母集団よりもサンプルサイズが小さくなるので、標本データ分散は母分散よりも小さくなる。それなので標本データ分散を母分散として用いることはできない。そこで標本データ分散を母分散と等しくなるように補正した不偏分散を母分散の推定量とする。
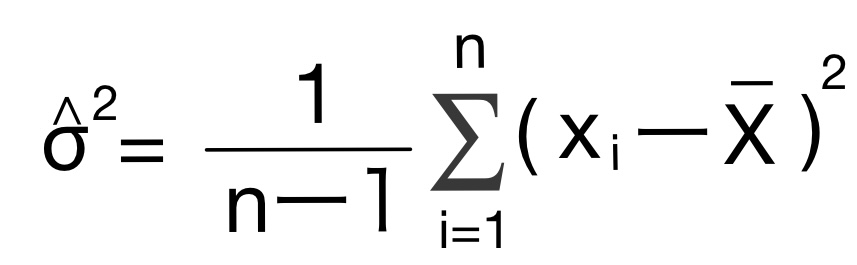
不偏分散はnではなくnー1で割ることで求められる。不偏分散によって標本から母分散を推定できるようになるのである。
t検定
正規分布に従うと仮定されたデータに対して仮説検定を行う場合、そのデータを標準化してZ値とすることでその正規分布を標準正規分布にして考える必要があった。
Z値に変換するには母分散が必要となってくるが、統計では母分散が未知であるという条件になっていることも多い。
そこで母分散が未知のときは代わりに不偏分散を母分散の推定量として用いる。
不偏分散を使って標準化したデータをt値と呼び、t値は標準正規分布ではなくt分布に従う。
t検定ではt値がt分布に従うことを利用して作られたt分布表から帰無仮説の下で検定統計量がその値となる確率であるp値を求めて、t値と予め決めていた有意水準を見比べて帰無仮説を棄却するかどうかを決める。
2標本t検定


そして、
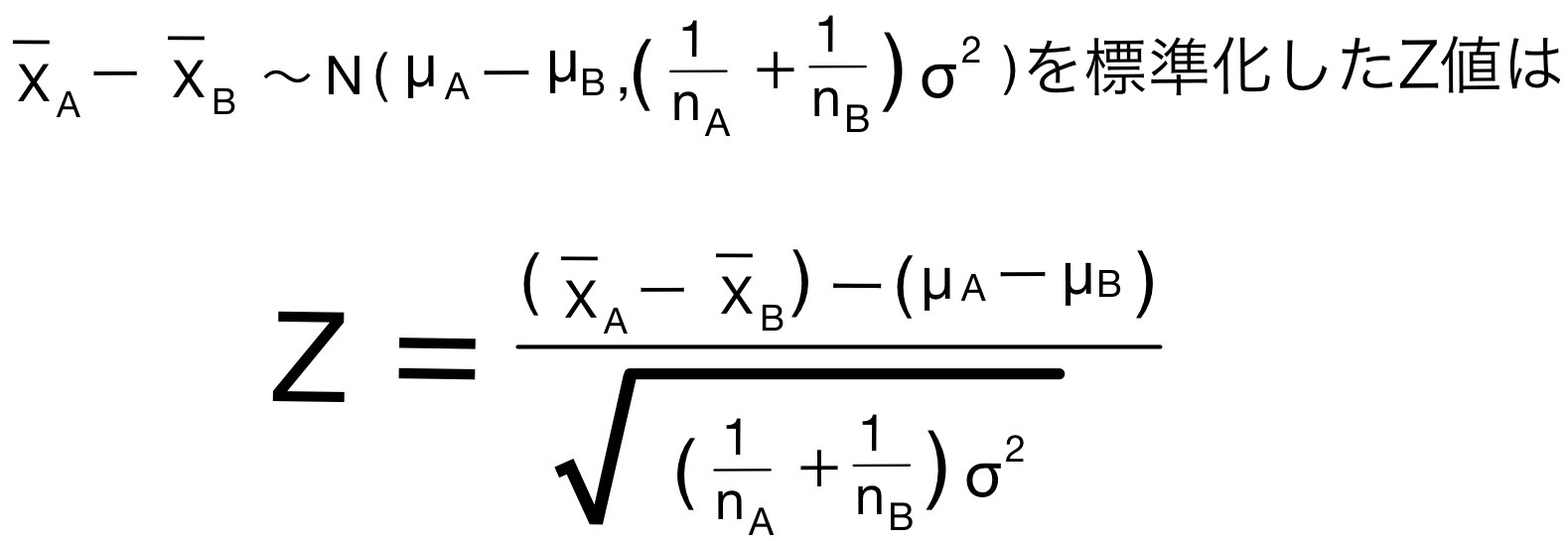
となりこれは標準正規分布N(0,1)に従う。
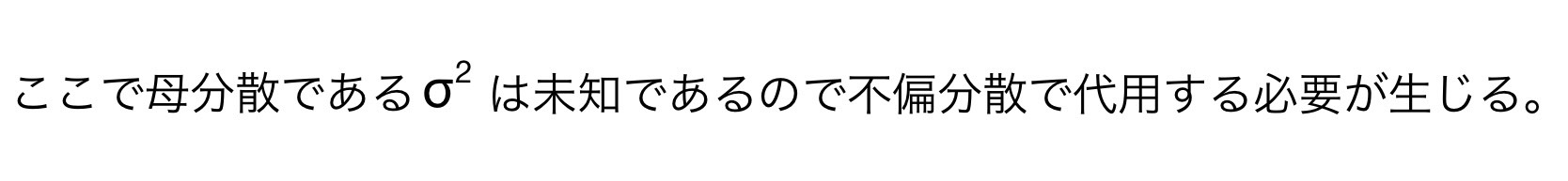
このときに考える不偏分散は母集団Aの標本データから求めた母集団Aの不偏分散と母集団Bの標本データから求めた母集団Bの不偏分散を混ぜたものになる。
この混ぜて作られた不偏分散を「プールされた不偏分散」という。

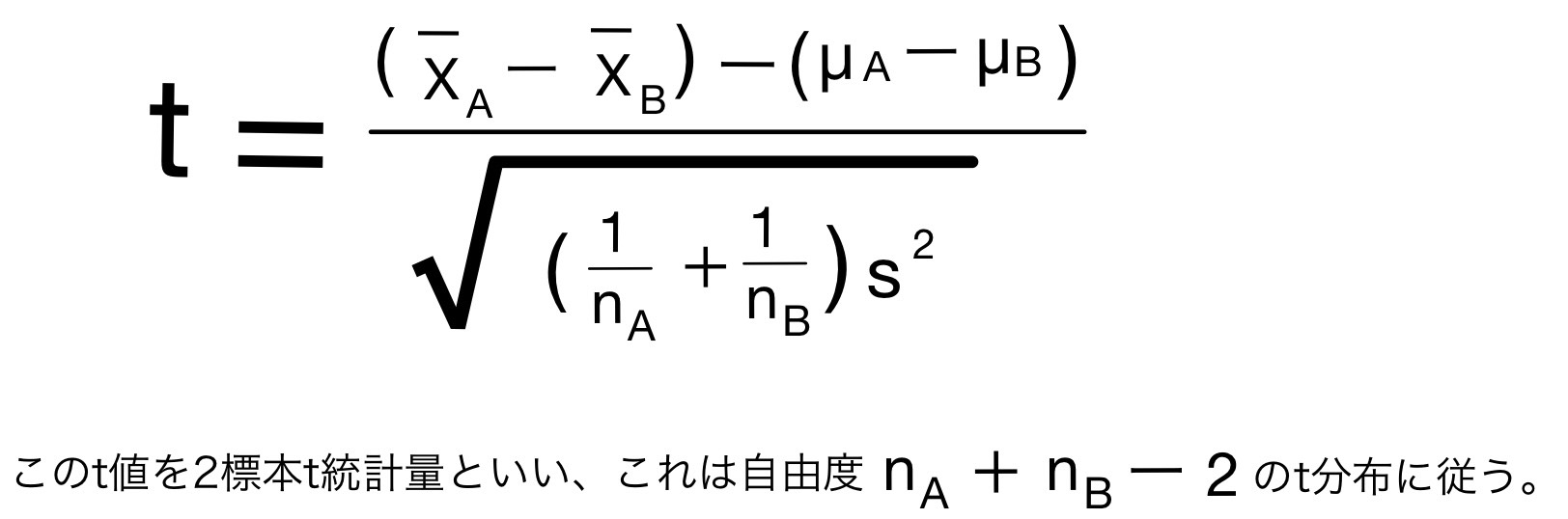
となる。式から分かるようにこの「プールされた不偏分散」はそれぞれの母集団の不偏分散が自由度によって重み付けされたものだと言える。
母分散を「プールされた不偏分散」で代用したものがt値である。



コメント