カイ2乗検定の流れ
カイ2乗検定とは帰無仮説を否定するための検定である。
「帰無仮説」とは証明したい仮説である「対立仮説」を証明するために否定されることを期待して立てる仮説である。文字通り「帰無仮説」を無に帰すことで対立仮説を証明する。
例えば「差がある」ことを証明したい場合は、「差がない」という仮説が帰無仮説となり「差がある」という仮説が対立仮説となる。
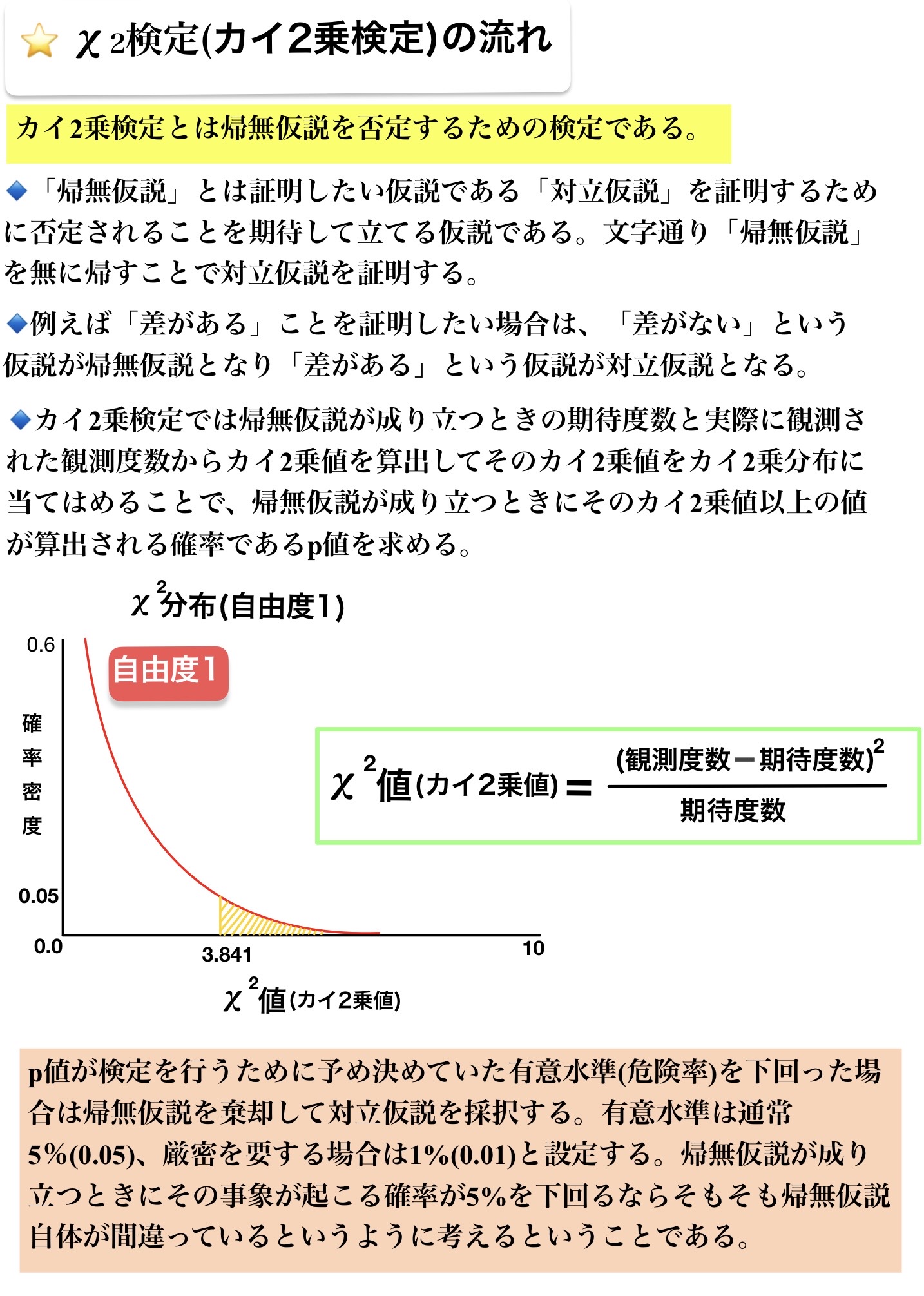
カイ2乗検定では帰無仮説が成り立つときの期待度数と実際に観測された観測度数からカイ2乗値を算出してそのカイ2乗値をカイ2乗分布に当てはめることで、帰無仮説が成り立つときにそのカイ2乗値以上の値が算出される確率であるp値を求める。
p値が検定を行うために予め決めていた有意水準(危険率)を下回った場合は帰無仮説を棄却して対立仮説を採択する。有意水準は通常5%(0.05)、厳密を要する場合は1%(0.01)と設定する。帰無仮説が成り立つときにその事象が起こる確率が5%を下回るならそもそも帰無仮説自体が間違っているというように考えるということである。
統計的有意差と臨床的意義

カイ2乗検定での統計的に有意になる差(統計的有意差)は、比較しているもの同士の差とデータ数(症例数など)で大きく変わってくる。
比較しているもの同士の差が臨床的意義がないほど小さなものだったとしても、カイ2乗値を算出する式から分かるようにデータ数(症例数など)が多いほどカイ2乗値は大きくなっていき、その差は統計的には有意となる差となってしまうのである。
そのため、統計的有意差イコール臨床的意義のある差と考えてはいけないのである。
疫学研究では研究を開始する前段階で最も評価したい主要評価項目(primary endpoint)に対する治療効果を推定して、それに合った症例数を設定する必要がある。
実際にカイ2乗検定をやってみる
生徒の総数が一学年100人である某医学部の解剖学の試験では毎年40%、つまり40人が落ちるような難易度に試験が設定されて実際に毎年40人ぐらいが落ちていた。しかし、今年試験をやってみると50人が落ちてしまった。解剖学の試験の難易度は例年と何ら変わらないものだったので解剖学の教員は50人という人数が多いと思い、今年の生徒の質が例年と比べて劣っていたとかいうような、とにかく今年と例年では「差があった」のではないかと考えてカイ2乗検定を行った。
この場合は帰無仮説が「差がなかった」という仮説になり、対立仮説が「差があった」という仮説となる。
カイ2乗値は帰無仮説が成り立つときの期待度数と実際に観測された観測度数から求められる。
今回のケースでは期待度数が合格者60人・不合格者40人であり、観測度数が合格者50人・不合格者50人であるのでカイ2乗値は4.17となる。

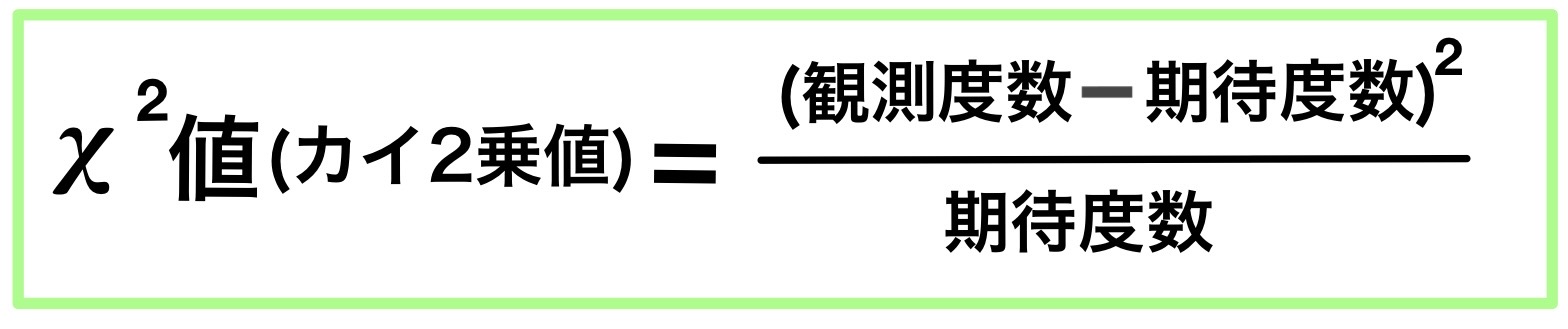
カイ2乗値は自由度によるカイ2乗分布に従う。
自由度とは「ある代表値や合計値があるときに自由に値をとれる数」と定義される。
このケースでの自由度は今年の合格者数を決めると自動的に今年の不合格者数が決まることから分かるように、自由に値を取れる数=自由度は1であることが分かる。
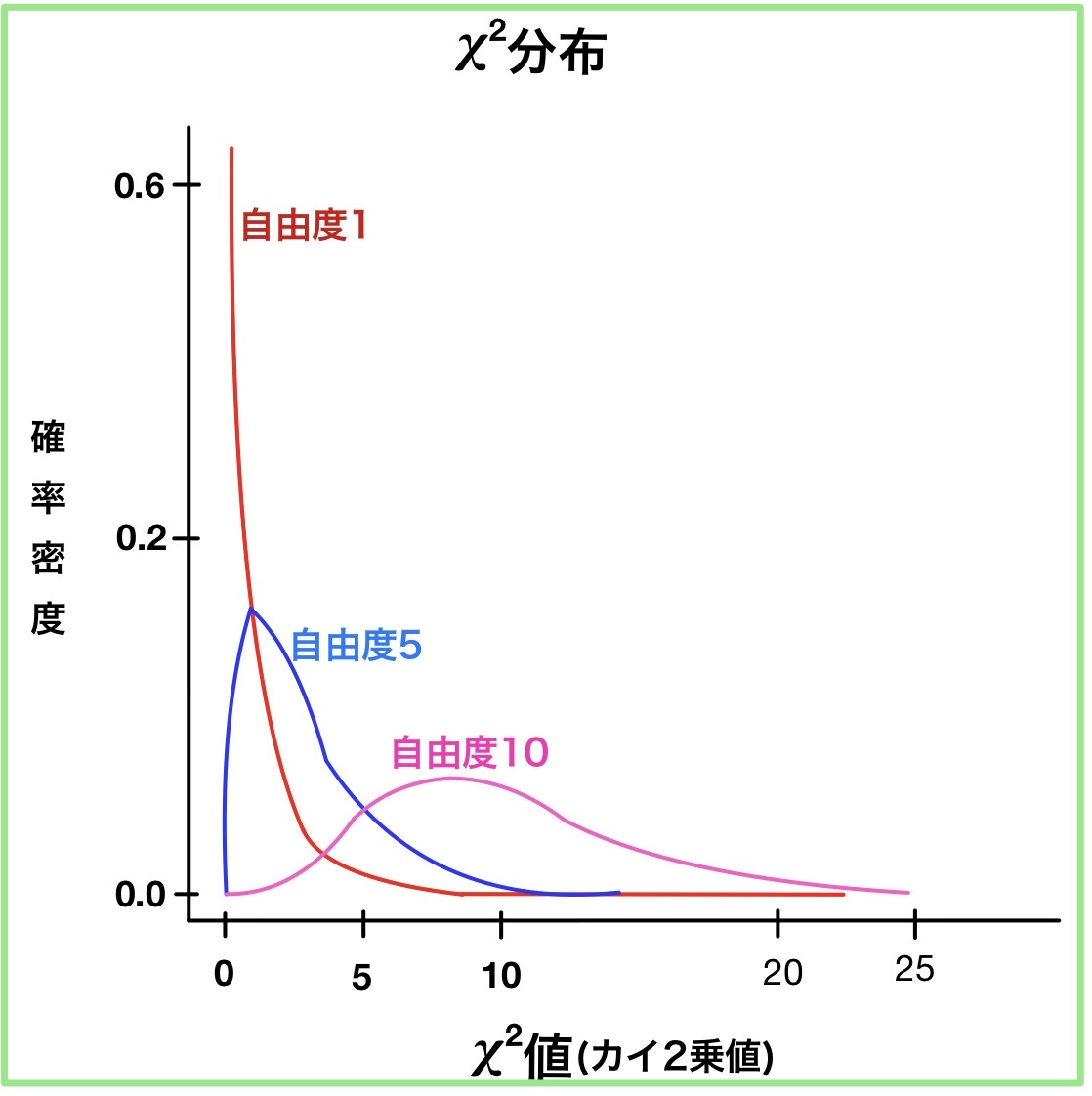
このように自由度によってカイ2乗分布は異なる。
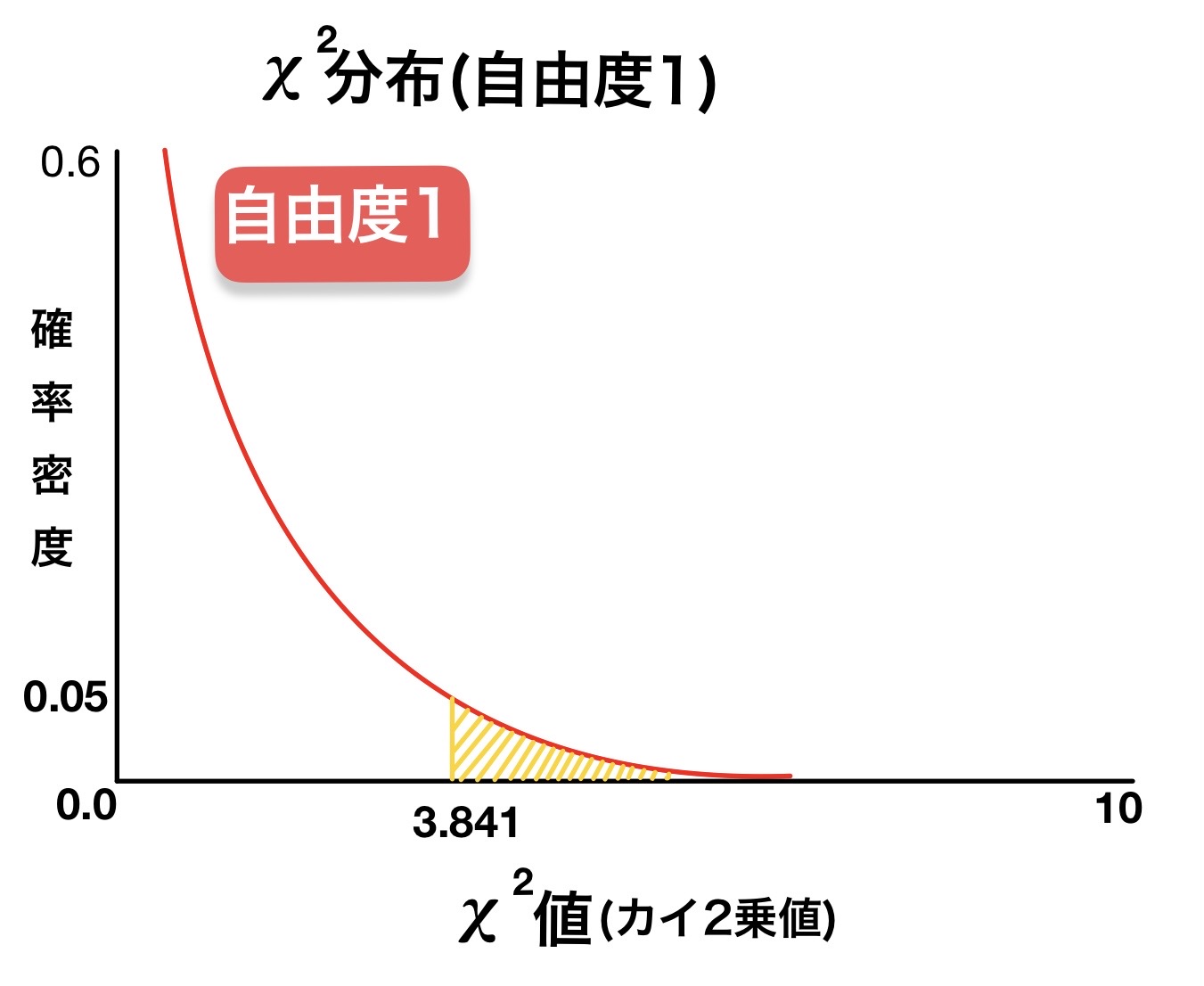
カイ2乗分布では確率が面積で表されており、例えば自由度1のカイ2乗分布ではカイ2乗値=3.841以上の面積の合計が5%でありカイ2乗値=3.841以上になる確率が5%以下になることを表す。
カイ2乗値とは計算式から分かるように「期待されたもの=帰無仮説からどれだけ離れているか」を表すので、カイ2乗値が大きいほど帰無仮説は遠のいていき対立仮説が近づいてくる。カイ2乗値をカイ2乗分布に当てはめて分かるp値を検定する前に決めた有意水準と比べて帰無仮説を棄却して対立仮説を採択するかどうか決める。
話を戻すが今回のケースでは自由度1,カイ2乗値=4.17であるので、p値=0.04となり有意水準を0.05に設定していた場合は帰無仮説が棄却されて対立仮説が採択される。
p値をどうやって算出したのかということになるが、自由度とカイ2乗値が分かったらp値はパソコンで計算できる。
これで感覚的に思っていた今年と例年では「差があった」ということがカイ2乗検定をすることで統計的に証明できた。
期待度数の求め方
上記の例では分かりやすいように期待度数を「合格者60人・不合格者40人」と決めつけているが、実際には期待度数もちゃんと計算して算出しないといけない。そこで期待度数を算出するまでの流れも含めてみる。
生徒の総数が一学年100人である某医学部の解剖学の試験では毎年40%、つまり40人が落ちるような難易度に試験が設定されて実際に毎年40人ぐらいが落ちていた。しかし、今年試験をやってみると50人が落ちてしまった。解剖学の試験の難易度は例年と何ら変わらないものだったので解剖学の教員は50人という人数が多いと思い、今年の生徒の質が例年と比べて劣っていたとかいうような、とにかく今年と例年では「差があった」のではないかと考えてカイ2乗検定を行った。
教員は今年が101回目の解剖学の試験であったため、これまで行われてきた100回の試験の合計の合格者数と不合格者数のデータを用いて今年と例年を比べた。
これまで行われてきた100回の試験の合計の合格率はぴったり60%であり、100回の試験の合計の合格者数=6000人・不合格者数=4000人であった。
まず今年の群と例年の群に分けて2×2表を作成する。
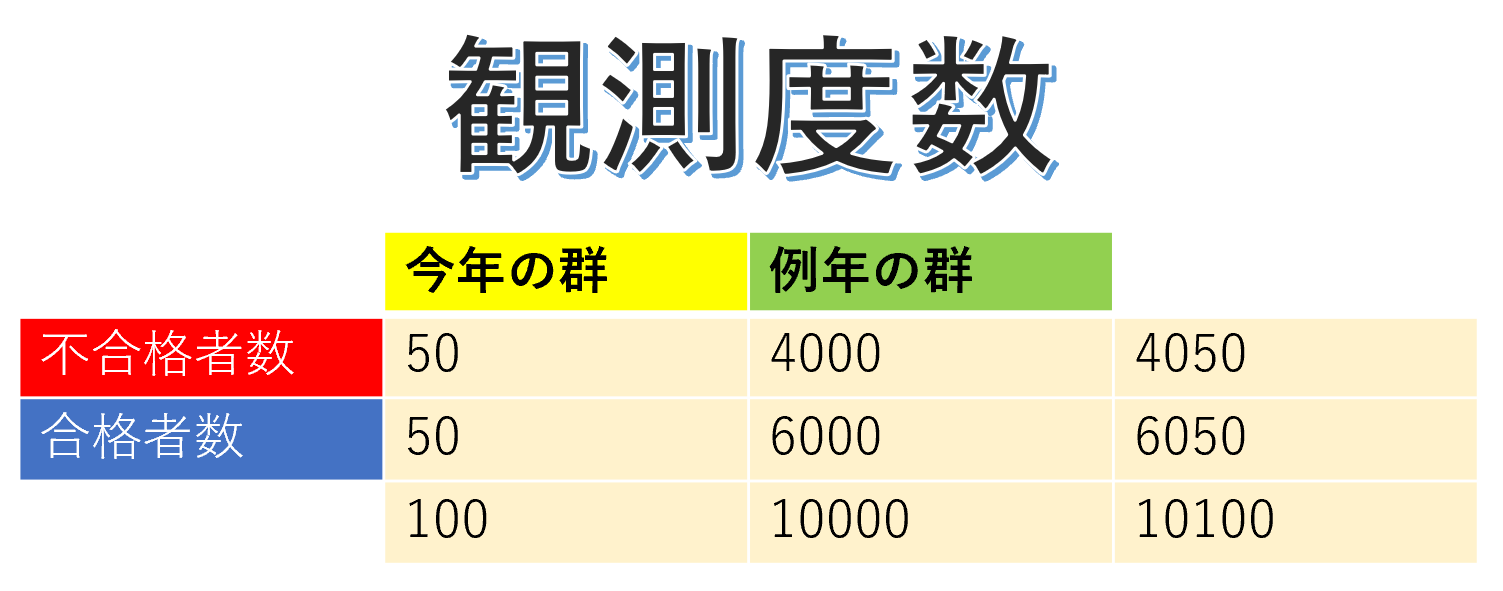
次に期待度数を求める。期待度数とは帰無仮説が成り立つときに「期待される数」のことである。
このケースでの帰無仮説は「今年と例年では差がない」という仮説なので、「全101回の試験の合計の不合格者数と合格者数」はそれぞれ「今年の群:例年の群=1:100の比」で構成されていることになる。

不合格者総数と合格者総数が決まっていて「今年と例年では差がない」場合にどうなるだろうかと考えると期待度数を算出しやすい。
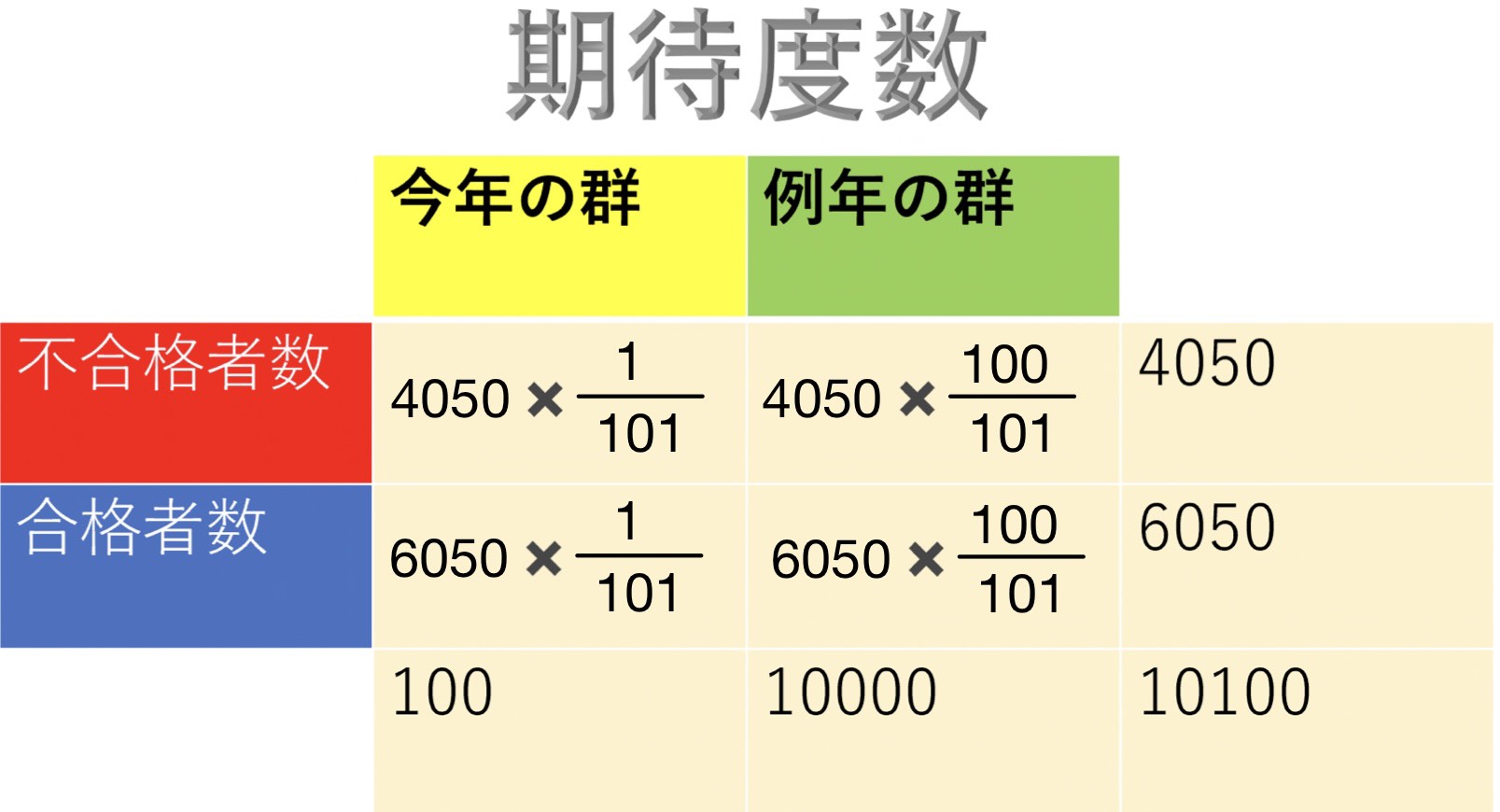
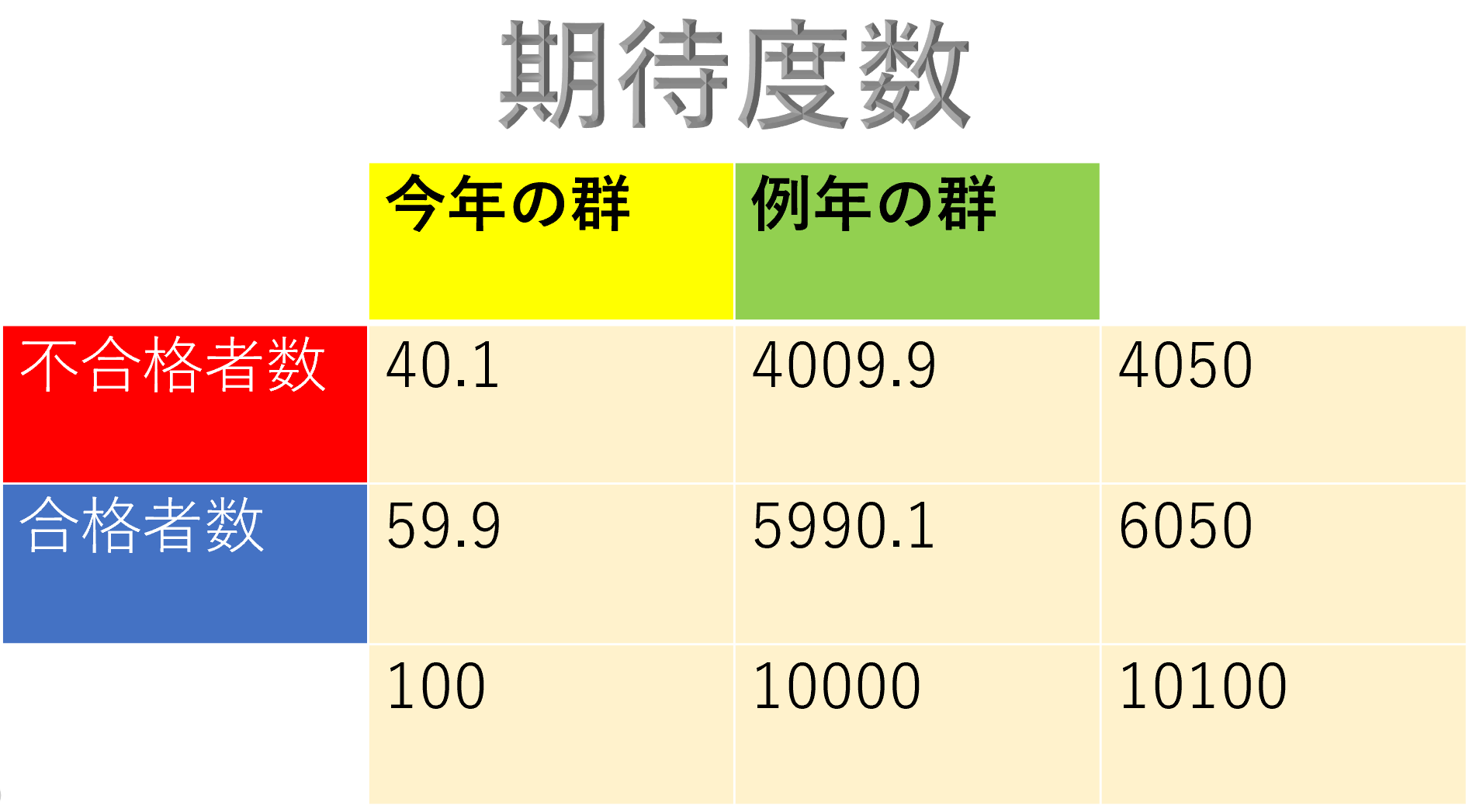
期待度数が分かったらカイ2乗値を算出する。

自由度1,カイ2乗値=4.1208からp値をパソコンで算出するとp値=0.0423となる。
よって、有意水準を0.05に設定していた場合は帰無仮説が棄却されて対立仮説が採択される。



コメント