公衆衛生・疫学計算問題対策
割合・率・比について
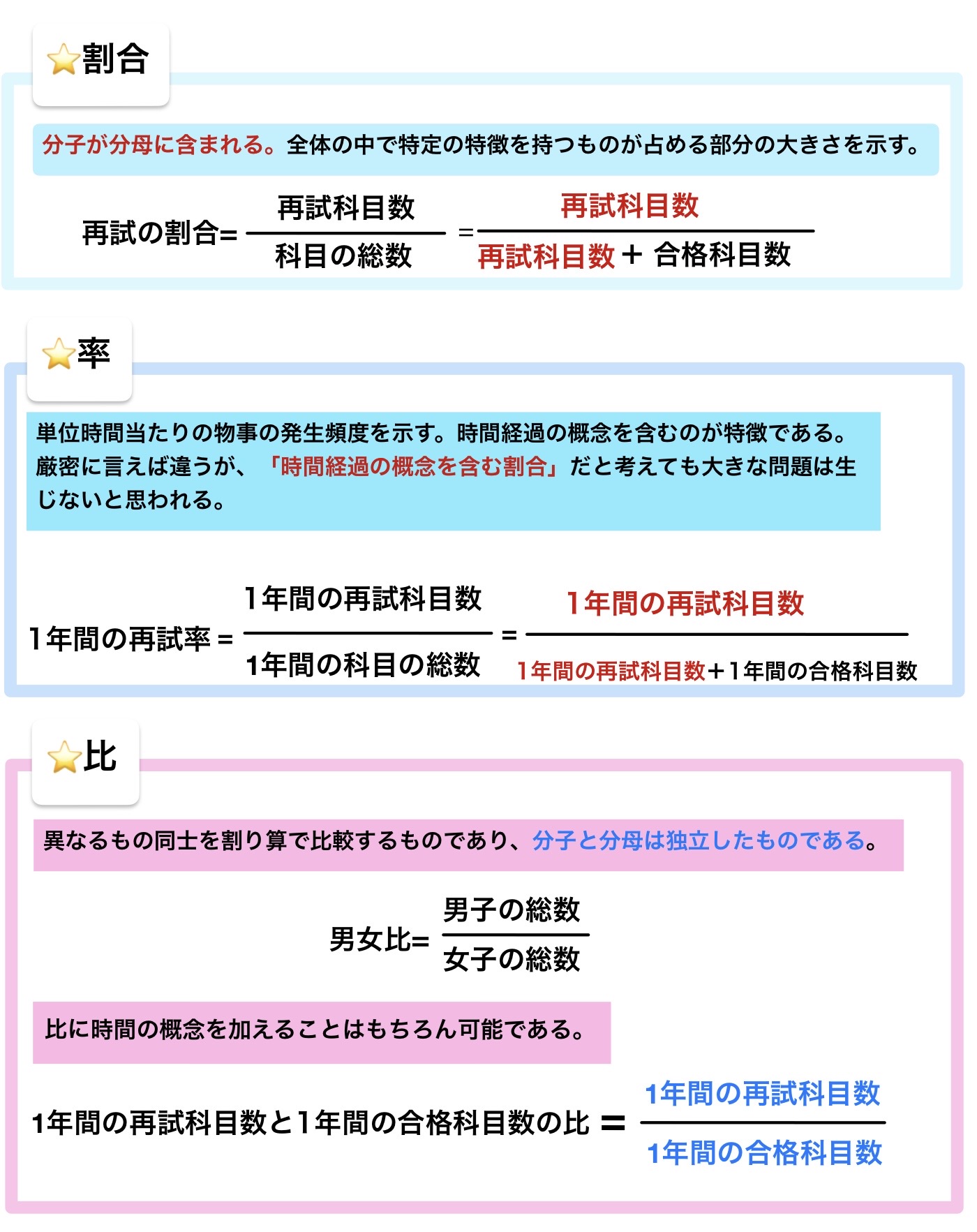
- 率の算出では分子は分母に含まれる。
- 比の算出では分子と分母とは独立である。
- 率の算出には時間的な概念が入ることがある。
- 比の算出には時間的な概念が入ることがある。
- 率と比は同じ意味で使用できる。
解答:5
解説:ややこしいのだが日本語には「比率」という言葉があり、これは「割合」の意味で使用される。しかし、「比」と「割合」は明確に区別されるので割合に時間の概念を加えたものと考えられる「率」を「比」と同じ意味で使用することはできない。
有病率と罹患率と死亡率

有病率
- 死亡率
- 出生率
- 致命率
- 有病率
- 罹患率
解答:4.有病率
解説:有病率は名前に「率」とついているが、ある一時点での疾病の頻度を示すものであり「割合」である。有病率は「割合」であるのである一時点での健康問題の「大きさ」を把握することはできる。しかし、有病率は時間経過の概念を含まない。それなので、疾病と発生要因との因果関係を探る場合は時間経過の概念を含む罹患率が適している。
2012年度保健師国家試験問題:有病率を低下させる要因はどれか?
- 罹患率が高くなる
- 平均有病期間が長くなる
- 観察集団から健康な人が流出する
- 重症化して短期間に死亡する人が増える
解答:4.重症化して短期間に死亡する人が増える
問題:ある一時点における再試保有者割合(再試を1つでも抱えた人の割合)を低下させる要因はどれか?2つ選んで下さい
[上記の2012年度保健師国家試験問題を理解するための問題]
- 本試が難しくなった
- 再試日が延期された
- 編入試験で天才が入学してきた
- 再試が本試よりも格段に難しくなるよう設定されることが決まり、再試のストレスに耐えられず病んでしまい退学する人が増えた
解答:3.編入試験で天才が入学してきた・4.再試が本試よりも格段に難しくなるよう設定されることが決まり、再試のストレスに耐えられず病んでしまい退学する人が増えた
解説:

選択肢1.について
本試が難しくなった場合再試保有者が増えるので再試保有者割合は当然上昇する。
選択肢2.について
再試を受けると留年する可能性は残るものの再試保有者というステータスからは外れる。ところが再試日が延期されてしまうと再試保有者というステータスに変わらずいることになるので、再試保有者割合が上昇する要因となる。
選択肢3.について
天才は再試には無縁だと思われるので、再試保有者数が増えないことが保証されたまま生徒の総数だけが増えることになる。この場合は再試保有者割合が低下する要因になる。
選択肢4.について
再試保有者が退学した場合は生徒の総数が減るものの再試保有者数も減るので、結果として退学する前と比べて再試保有者割合は低下する。
罹患率・死亡率

問題:2017年から2021年にかけて疾患Xについて調査を行った。対象者は100人である。2017年に疾患Xを20人が発症した。2018年にさらに20人が疾患Xを発症した。2019年に疾患X罹患者のうち3人が死亡した。2020年に疾患X罹患者のうちさらにもう1人が死亡した。
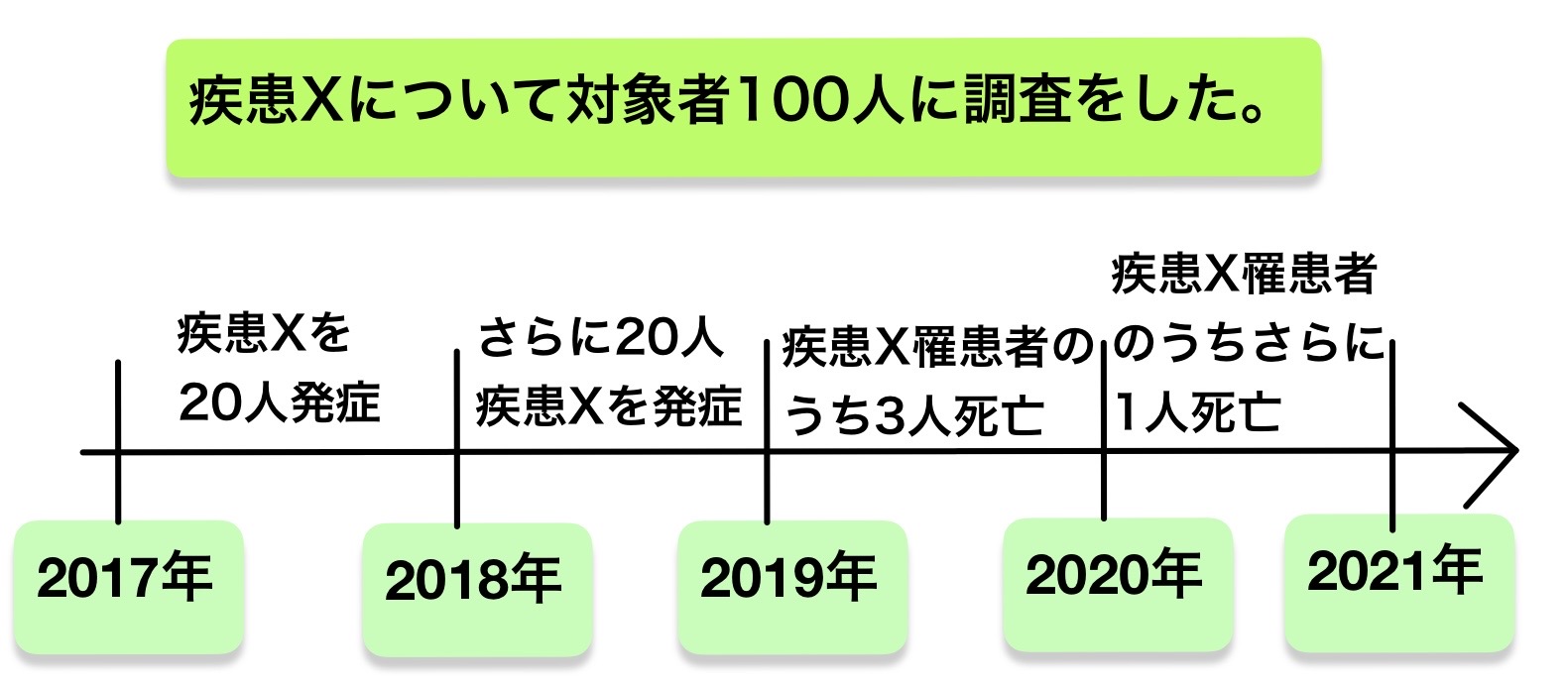
観察期間内での罹患率・累積罹患率を求めよ。

104G68:都市Aは人口50万人で、疾患Bの登録事業を実施している。2008年の初めの時点での疾患Bの患者数は120人、2008年に疾患Bが新たに発症したのは40人、疾患Bが治癒したのは20人、疾患Bで死亡したのは30人であった。
都市Aにおける2008年の疾患Bの罹患率(人口10万対)はどれか。
- 4
- 6
- 8
- 20
- 24
- 32
- 50

10万人の0.008%は8人であるので、罹患率(人口10万対)は8である。10万人の0.008%は800人ではない。
実際の問題の解き方としては『50万人当たり40人発症したので、10万人当たり8人発症する』と考えれば早い。
問題:人口1000人のX町での10年間の死亡数は20人であった。このときのX町での死亡率(10万人年対)はどれか?
- 20人
- 100人
- 200人
- 400人

10万人の0.2%は200人であるので、死亡率(10万人年対)は200人となる。
「100人当たり10年間で20人死亡する→100000人当たり10年間で2000人死亡する→100000人当たり1年間で200人死亡する」と考えれば早い。
ROC曲線
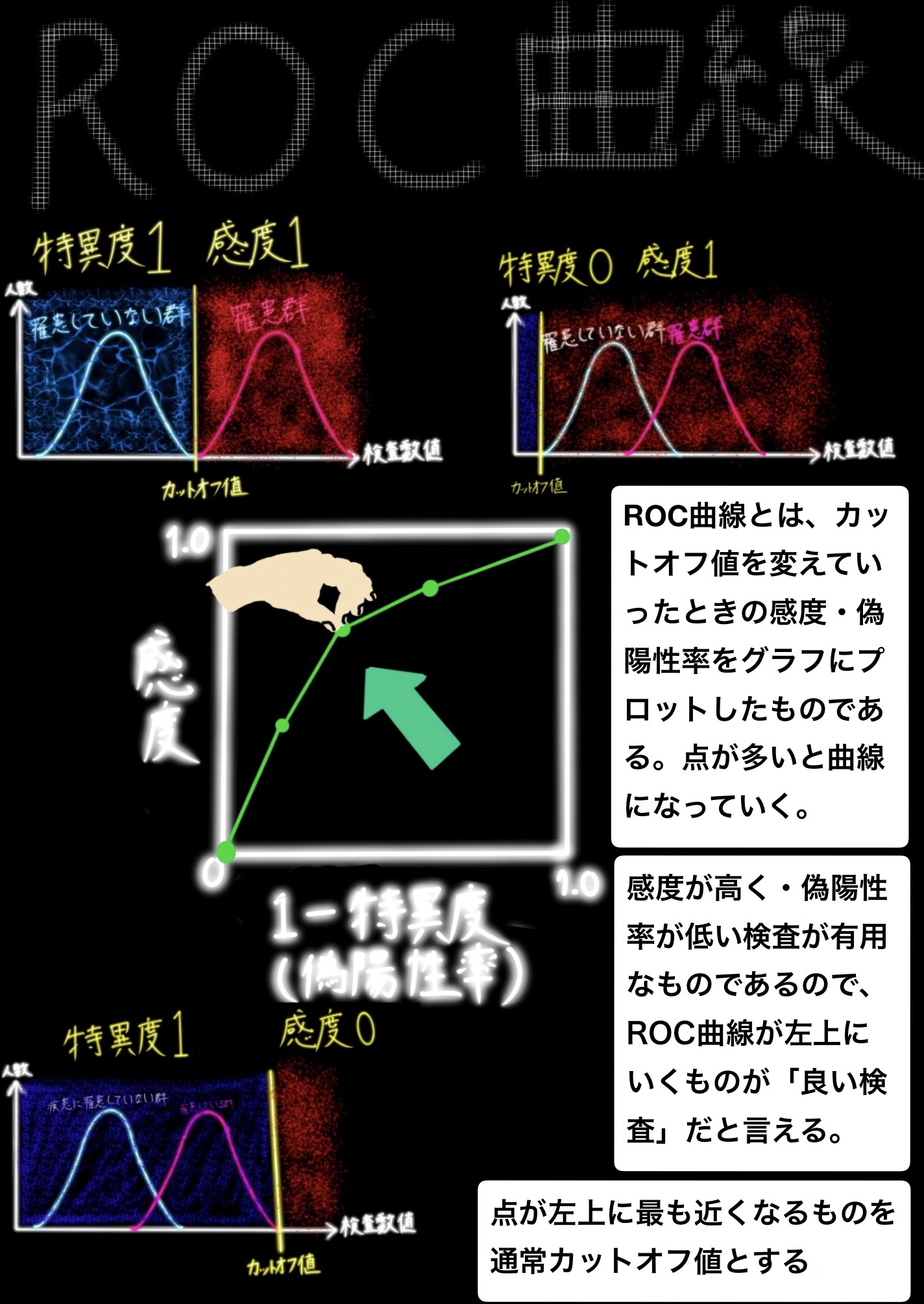
ROC曲線とは、カットオフ値を変えていったときの感度・偽陽性率をグラフにプロットしたものである。点が多いと曲線になっていく。
感度が高く・偽陽性率が低い検査が有用なものであるので、ROC曲線が左上にいくものが「良い検査」だと言える。
点が左上に最も近くなるものを通常カットオフ値とする。
検査前確率・検査後確率
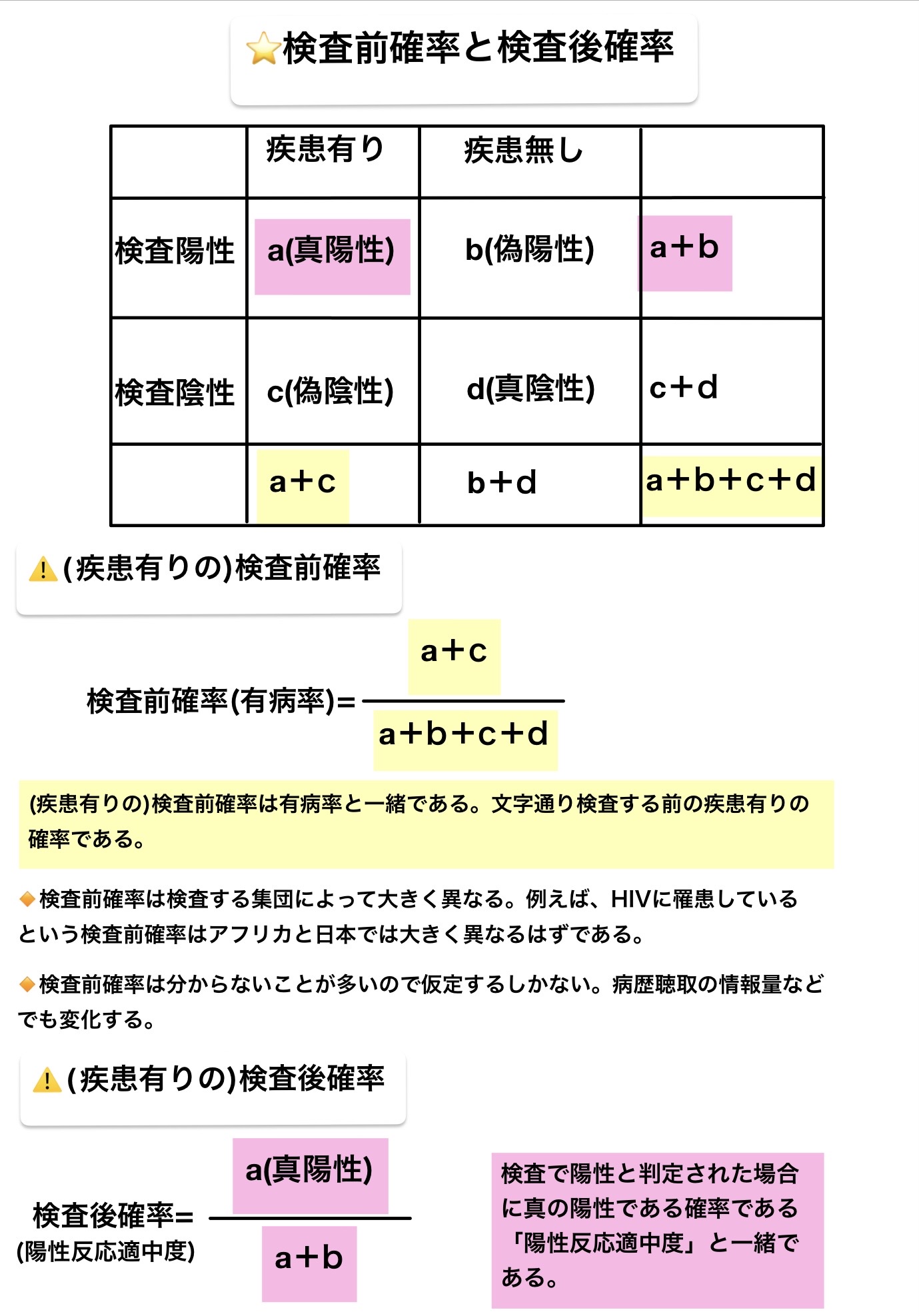
検査前確率は有病率と一緒である。文字通り検査する前の確率である。
検査前確率は検査する集団によって大きく異なる。例えばHIVに罹患しているという検査前確率はアフリカと日本では大きく異なることが想像できる。
検査前確率は分からないことが多いので仮定するしかない。病歴聴取の情報量などでも変化する。勝手に医師が推測することになることもある。
検査後確率は陽性反応適中度・陰性反応適中度を指し、主に陽性反応適中度の意味で使われる。
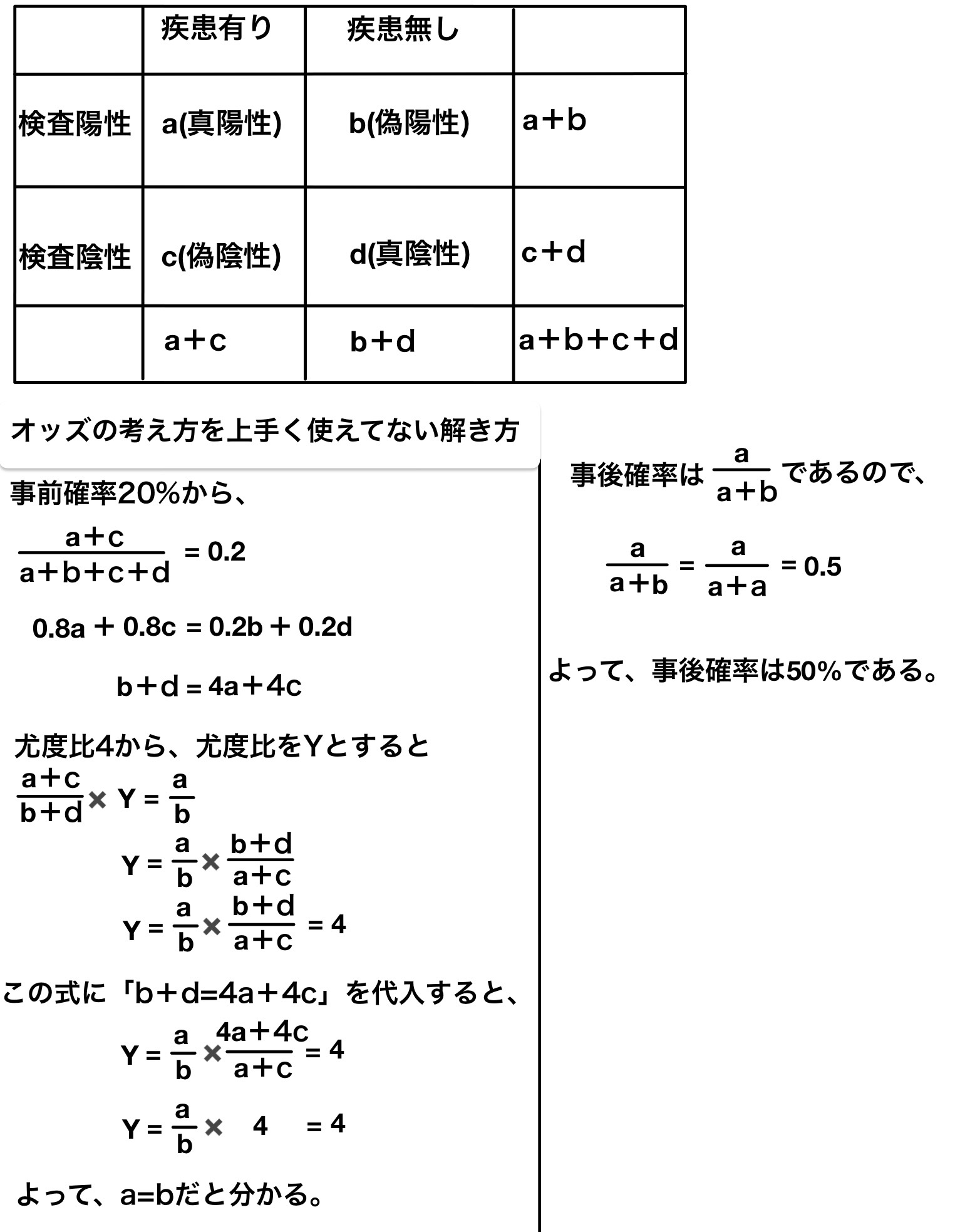
103F17:ある腫瘍マーカーを肺癌患者100人と非肺癌患者1,000人とで測定したところ、表のような結果が得られた。
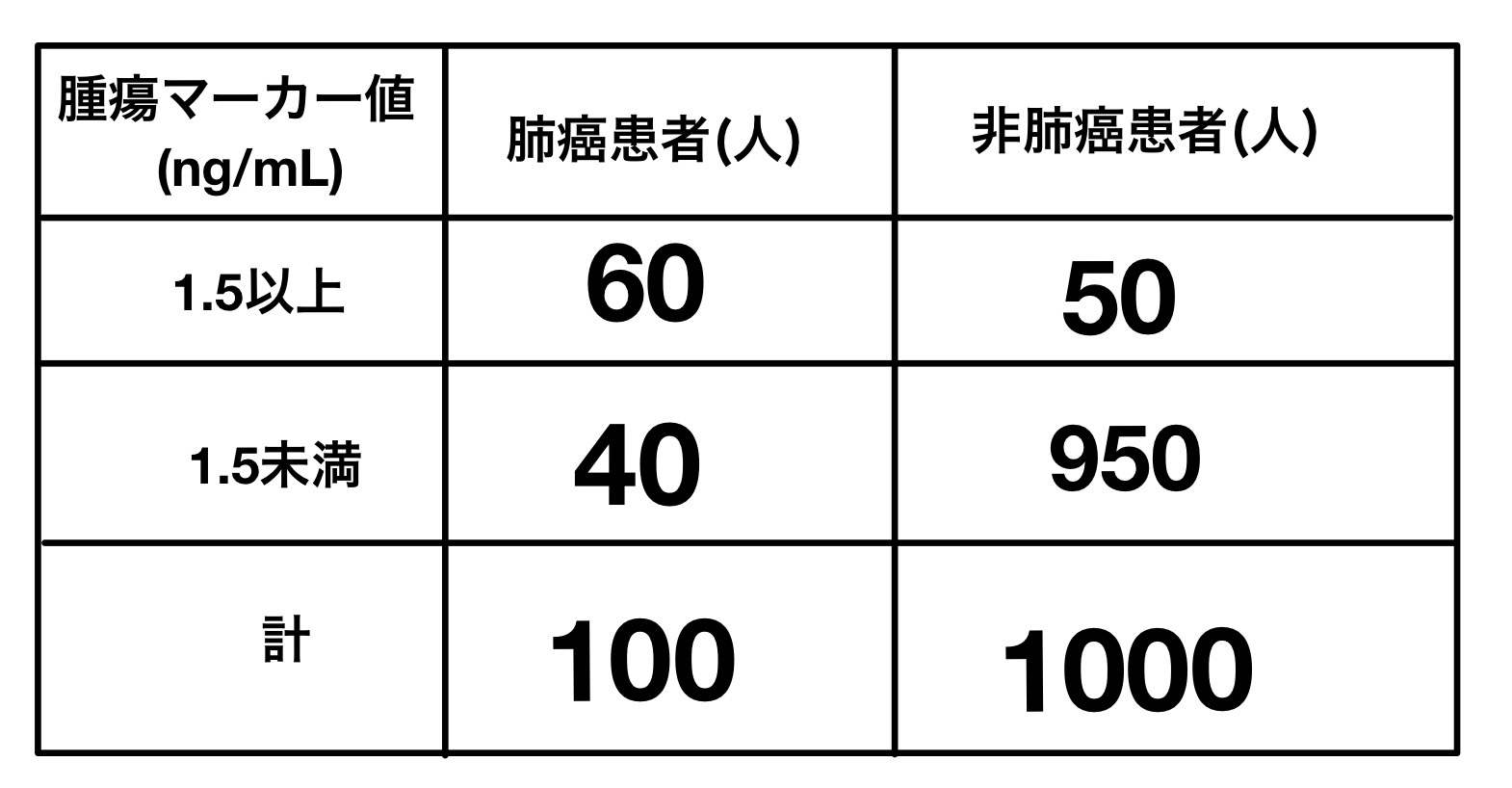
この測定値が2.0ng/mLのとき、肺癌である検査後確率はどれか。
ただし、肺癌の検査前確率を20%と仮定する。
- 20%
- 25%
- 50%
- 75%
- 80%
表は「肺癌患者をこの腫瘍マーカーで測定すると60%が1.5以上(肺癌陽性)で40%が1.5未満(肺癌陰性)」=「感度60%」・「非肺癌患者をこの腫瘍マーカーで測定すると5%が1.5以上(肺癌陽性)で95%が1.5未満(肺癌陰性)」=「特異度95%」であるということを意味している。
勘違いしてはいけないのは、この肺癌患者100人と非肺癌患者1000人の集団の中の人の測定値が2.0ng/mLのときの肺癌の検査後確率を求めているわけではないってこと。だって、この集団の中では肺癌の検査前確率は100÷1100×100=9.09%だからである。
問題では肺癌の検査前確率を20%と仮定しているから、その集団を新しく考えなくてはいけない。
「感度60%」・「特異度95%」・「検査前確率が20%」という集団を仮定すると、

上のやり方は解説するために一般化したものである。実際にはX=100,Y=400のような集団を考えると一瞬で解ける。「検査前確率=20%」から「Y=4X」だなとすぐ分かることができれば早い。
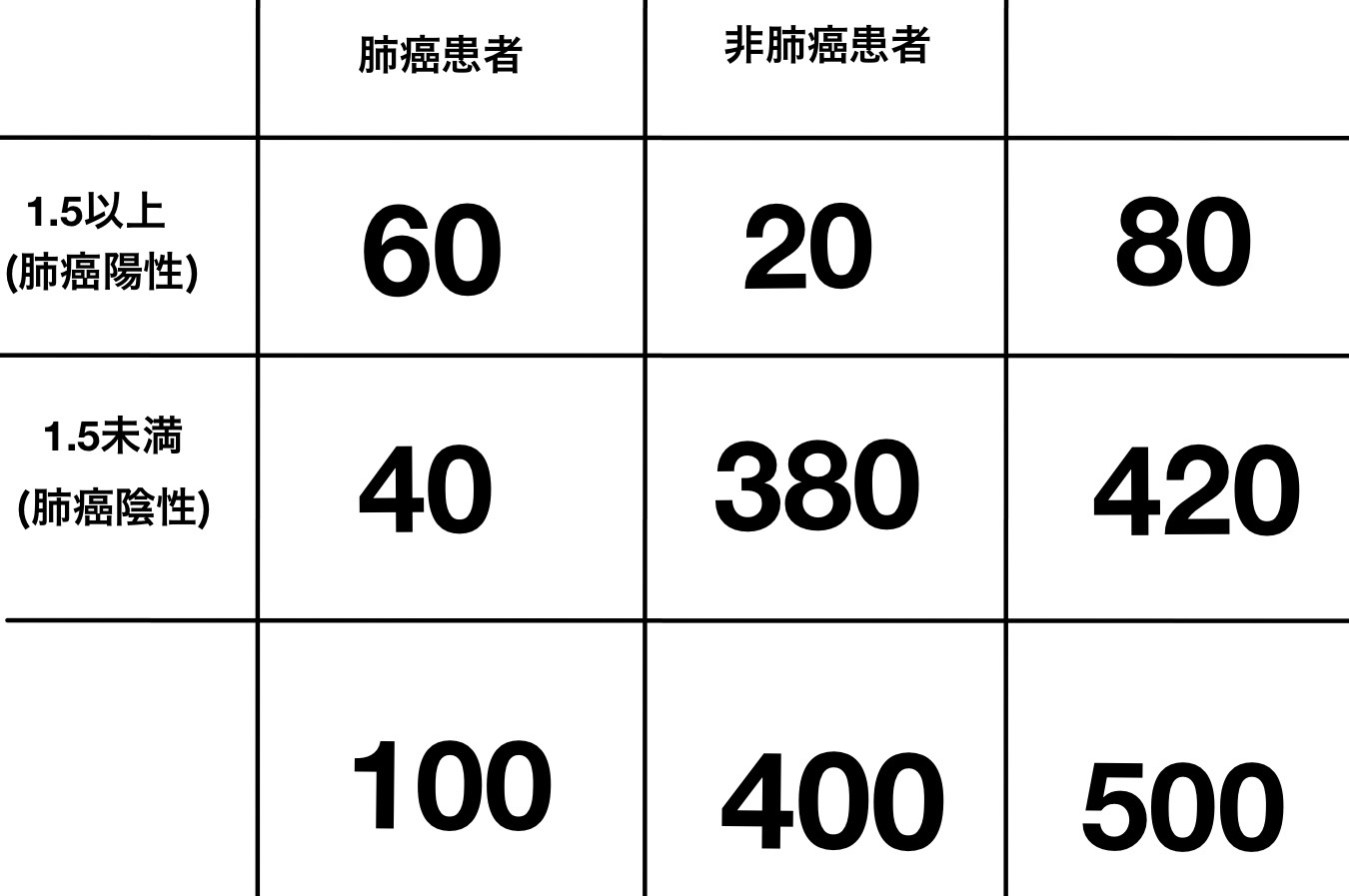
99C13:45歳の男性.腹痛のため来院した.1週前から上腹部と背部とに強い痛みがあり,食事ができなくなった.20歳ころから1日3合の日本酒をほぼ毎日飲んでいる.意識は清明.身長165cm,体重62kg.脈拍92/分,整.血圧110/72mmHg.顔面は苦悶様.背中を丸めるような姿勢をしている.腹部聴診では腸雑音が減弱している.心窩部に圧痛を認める.尿所見:蛋白1+,糖(-),ケトン体3+,潜血(-).血液所見:赤血球442万,Hb 15.1g/dL,白血球10,900,血小板23万.血清生化学所見:総ビリルビン3.5mg/dL,AST 33単位,ALT 66単位,アミラーゼ94単位(基準37~160),Ca 8.6mg/dL.CRP 23.8mg/dL.
この患者が急性膵炎である検査前確率を50%としたときの検査後確率はどれか.血清アミラーゼの急性膵炎に対する感度は78%,特異度は88%とする.
- 11%
- 20%
- 28%
- 35%
- 43%
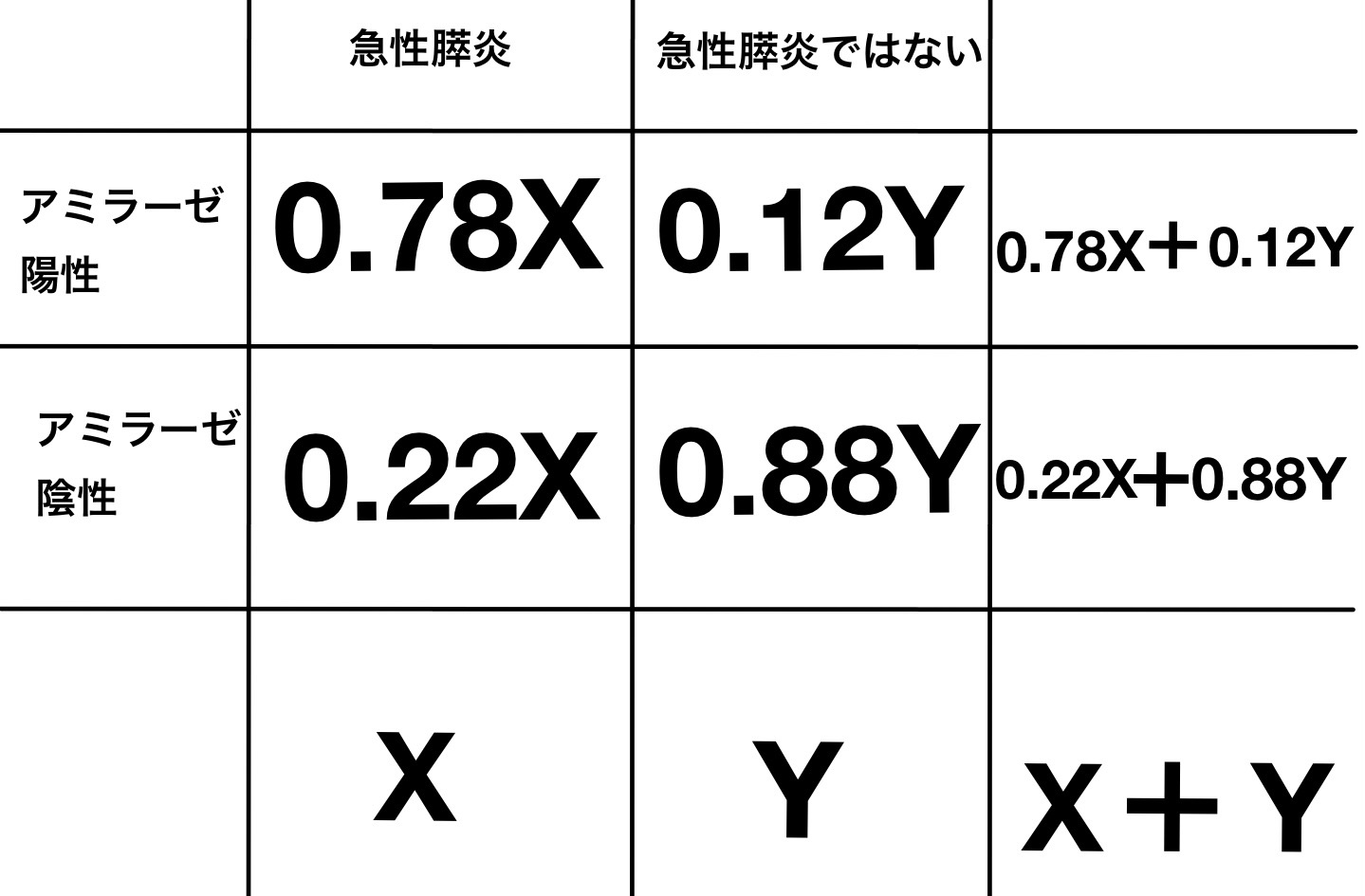
患者はアミラーゼ陰性なので偽陰性の確率(検査後確率)を調べる。
この集団では検査前確率が50%なので、

では、偽陰性の確率(検査後確率)は
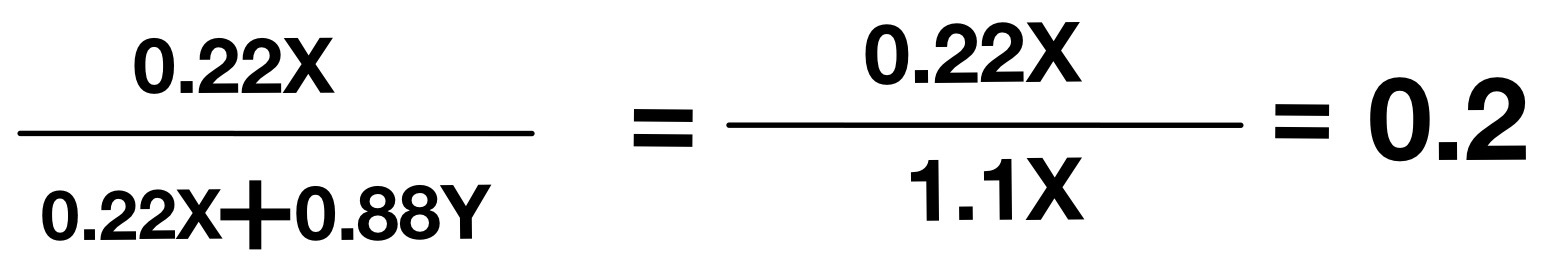
解答:20%
102B14:大腸癌に対して感度80%、特異度70%の検査がある。ある地区でこの検査を施行したところ、100人の陽性者が見つかった。
真に大腸癌を有すると予測される人数はどれか。
- 20人
- 30人
- 70人
- 80人
- 予測できない
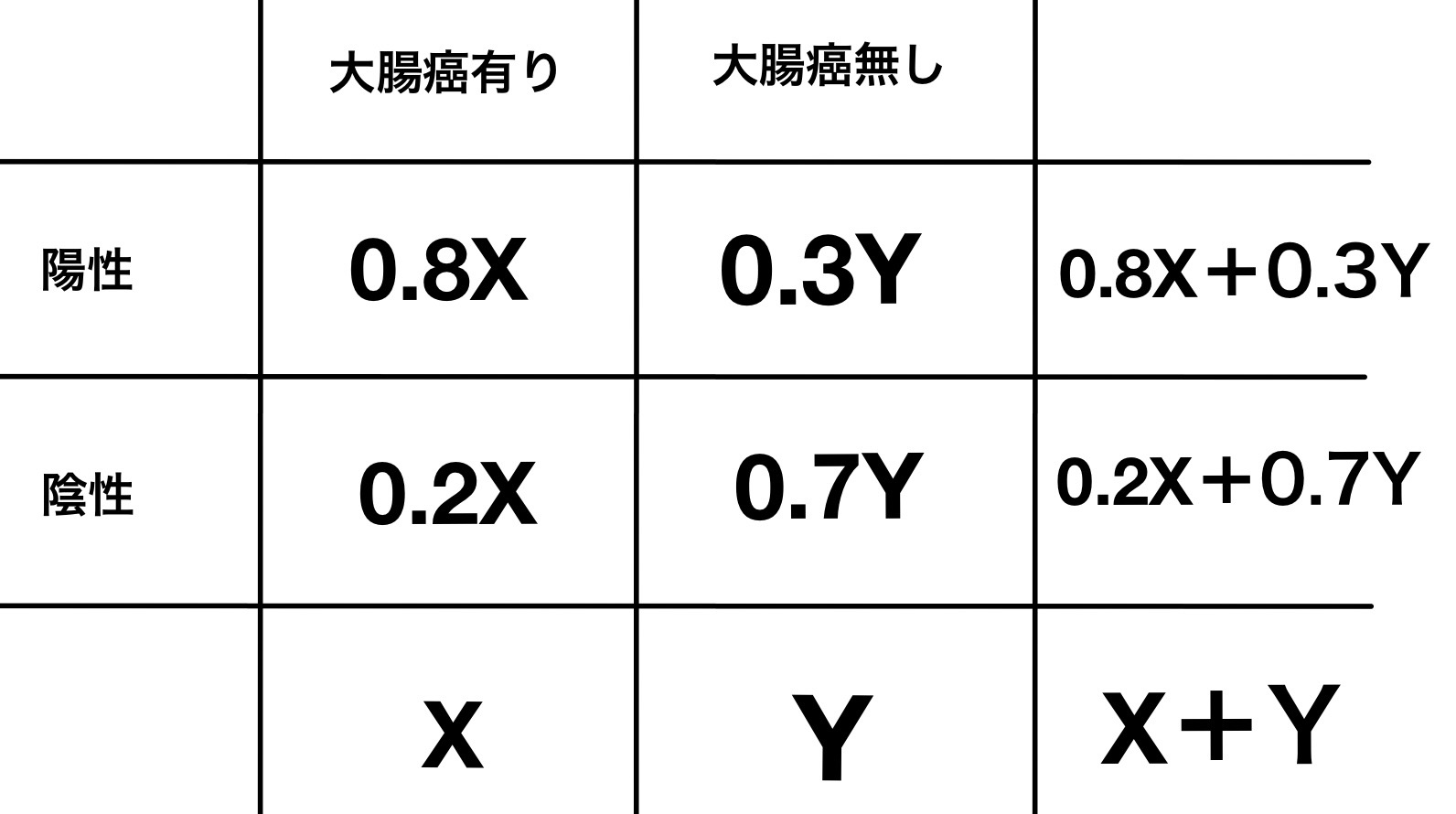
「0.8X+0.3Y=100」という情報のみから0.8Xを求めることはできない。もう一つ有病率などの式がないとX,Yを求めることができない。
よって答えは「5.予測できない」である。
陽性反応適中度
問題:有病率が0.6%の疾患Xについての検査の感度が70%、特異度が99%であった。この検査の陽性反応適中度を求めよ。

- 有病率=0.01、感度=0.99、特異度=0.50
- 有病率=0.01、感度=0.50、特異度=0.99
- 有病率=0.01、感度=0.99、特異度=0.99
- 有病率=0.50、感度=0.99、特異度=0.50
- 有病率=0.50、感度=0.50、特異度=0.99
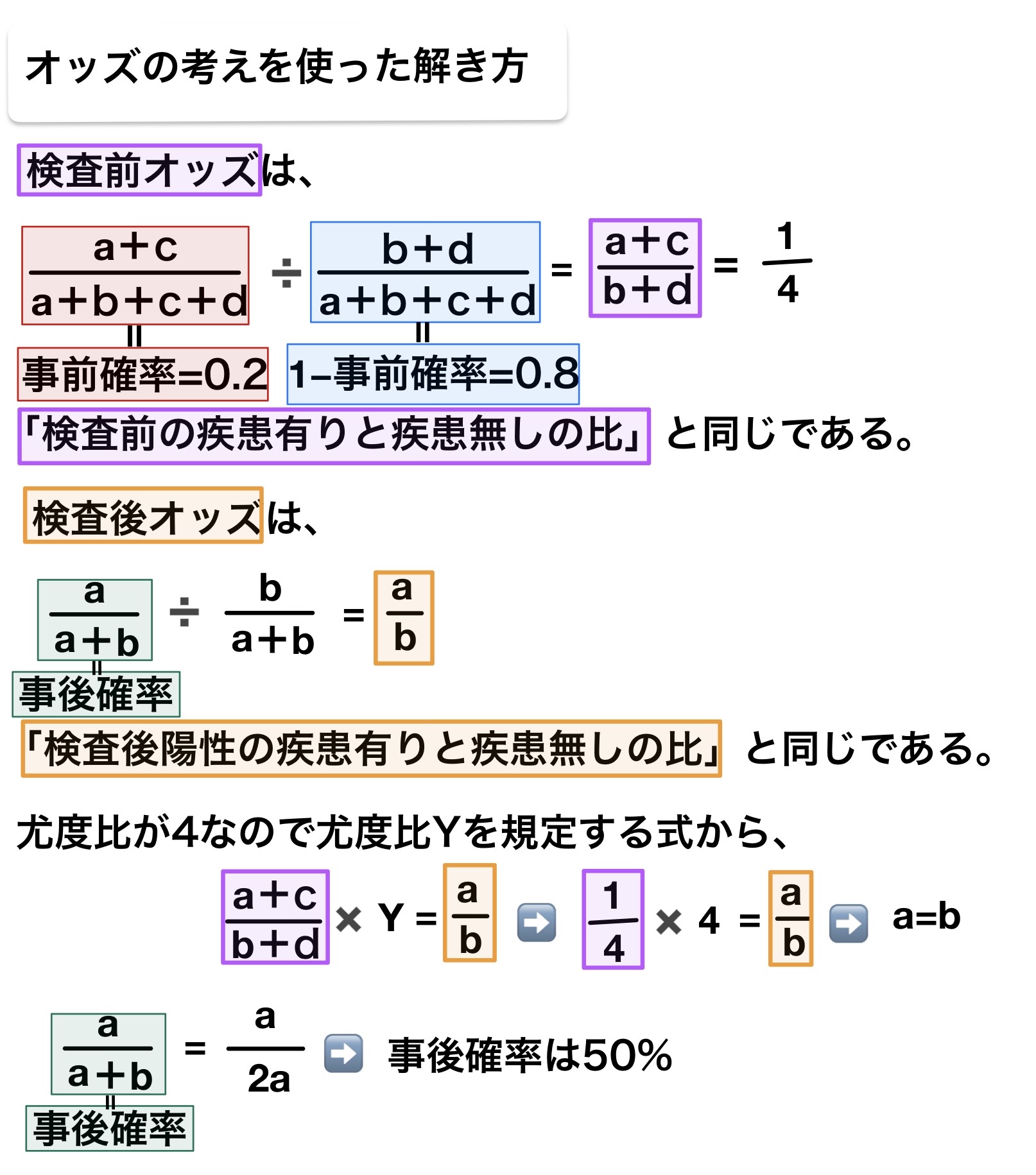
尤度比
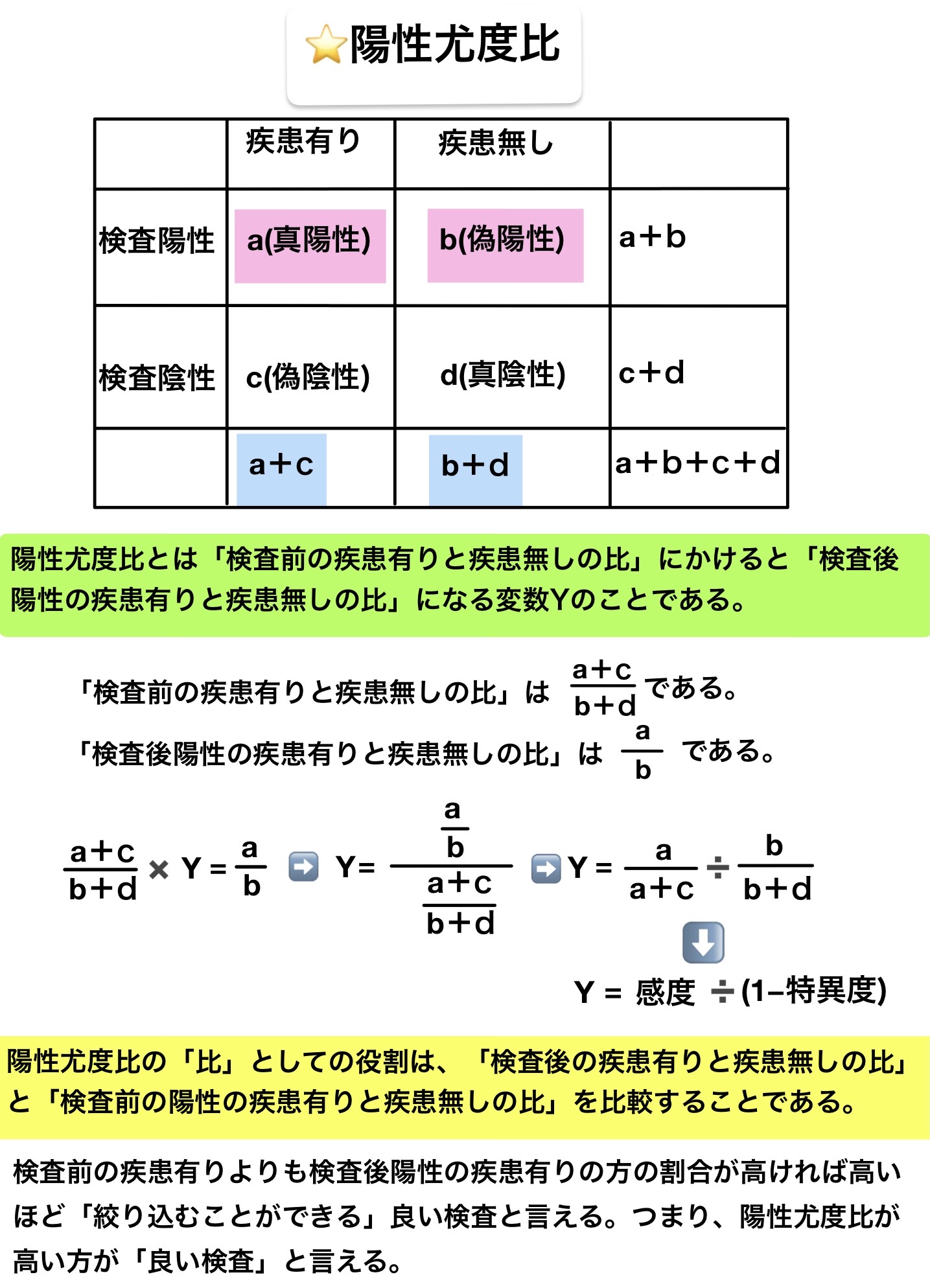
陽性尤度比とは「検査前の疾患有りと疾患無しの比」にかけると「検査後陽性の疾患有りと疾患無しの比」になる変数Yのことである。
陽性尤度比の「比」としての役割は、「検査後の疾患有りと疾患無しの比」と「検査前の陽性の疾患有りと疾患無しの比」を比較することである。
検査前の疾患有りよりも検査後陽性の疾患有りの方の割合が高ければ高いほど「絞り込むことができる」良い検査と言える。つまり、陽性尤度比が高い方が「良い検査」と言える。
- 0.3
- 0.5
- 1.3
- 2.0
- 4.8
解答:4,2.0
解説:0.8÷(1.0-0.6)=2.0
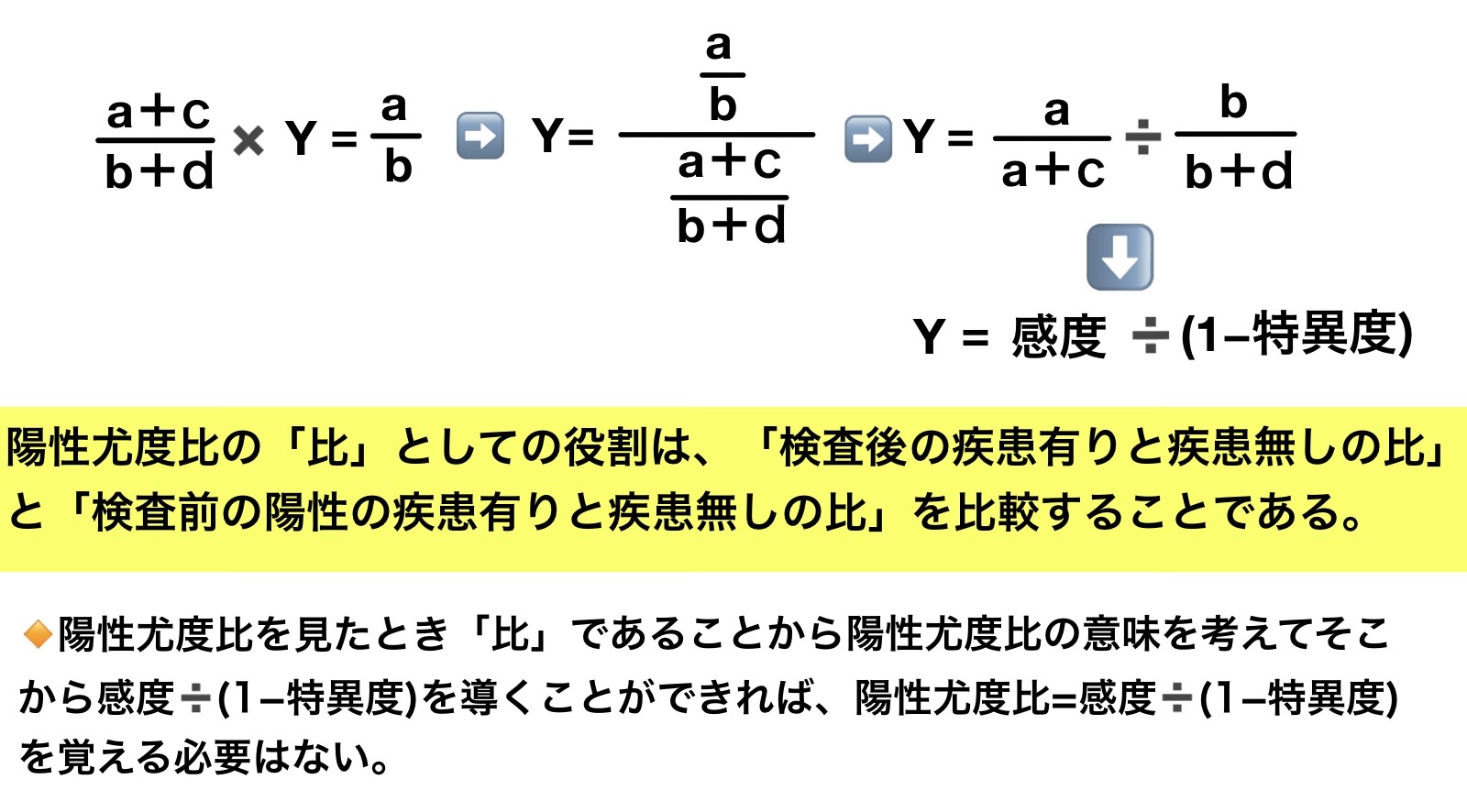
陽性尤度比を見たとき「比」であることから陽性尤度比の意味を考えてそこから感度➗(1−特異度)を導くことができれば、陽性尤度比=感度➗(1−特異度)を覚える必要はない。
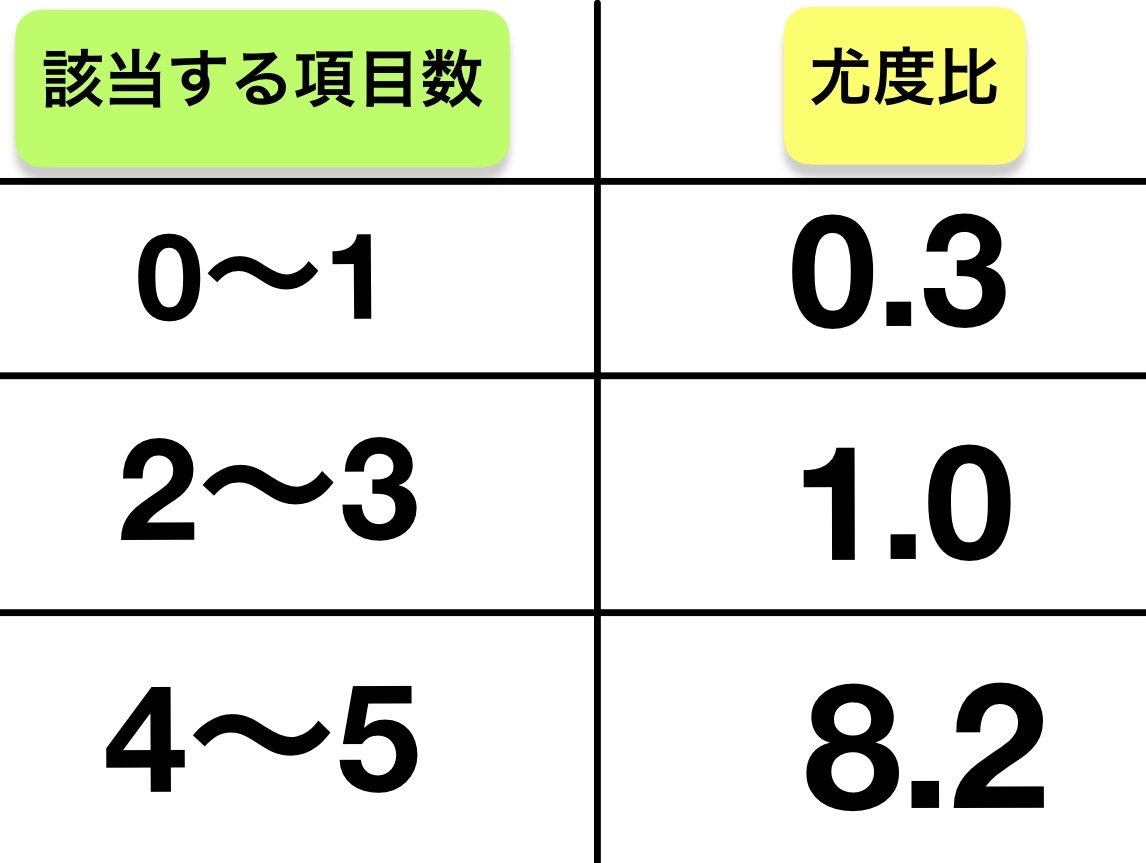
106H30:50歳の男性。発熱と咳とを主訴に来院した。3日前に咳が出現した。昨日から痰を伴うようになり、悪寒も自覚したため、救急外来を受診した。生来健康で、気管支喘息の既往はない。体温38.5℃。心拍数104/分、整。血圧110/70mmHg。呼吸数20/分。聴診上、右前胸部で呼吸音の減弱を認めた。coarse cracklesとwheezesとを認めない。肺炎の診断に関する文献を調べたところ、「気管支喘息がない」、「体温>37.8℃」、「心拍数>100/分」、「呼吸音が減弱している」、「coarse cracklesを聴取する」の5項目に該当する項目数によって、尤度比を予測できることが報告されていた。その対応関係を示す。
病歴と身体診察所見に基づき計算した場合に、検査前確率〈事前確率〉に比べた検査後確率〈事後確率〉の変化として適切なのはどれか。
- 低くなった。
- 高くなった。
- 変化しなかった。
- 診察前の確率による。
- 評価できない。
解答:2.高くなった。
該当する項目数が4つなので尤度比は8.2である。
尤度比8.2の場合、明らかに「検査後の方が疾患有りの割合が増えた」ということであるので検査後確率は高くなる。

109F10:事前確率が20%のときに尤度比4の所見があれば事後確率はどれか。
- 5%
- 16%
- 24%
- 50%
- 80%
相対危険度(リスク比:RR)
113F84:19世紀のロンドンで、激しい下痢を伴う、後にコレラと判明する疾患が大流行した。疫学者のJohn Snowは水道水との関連を疑い、詳しい調査を行った。調査の結果の概要を以下に示す。なお、表中のA、Bは異なる水系を持つ供給元である。
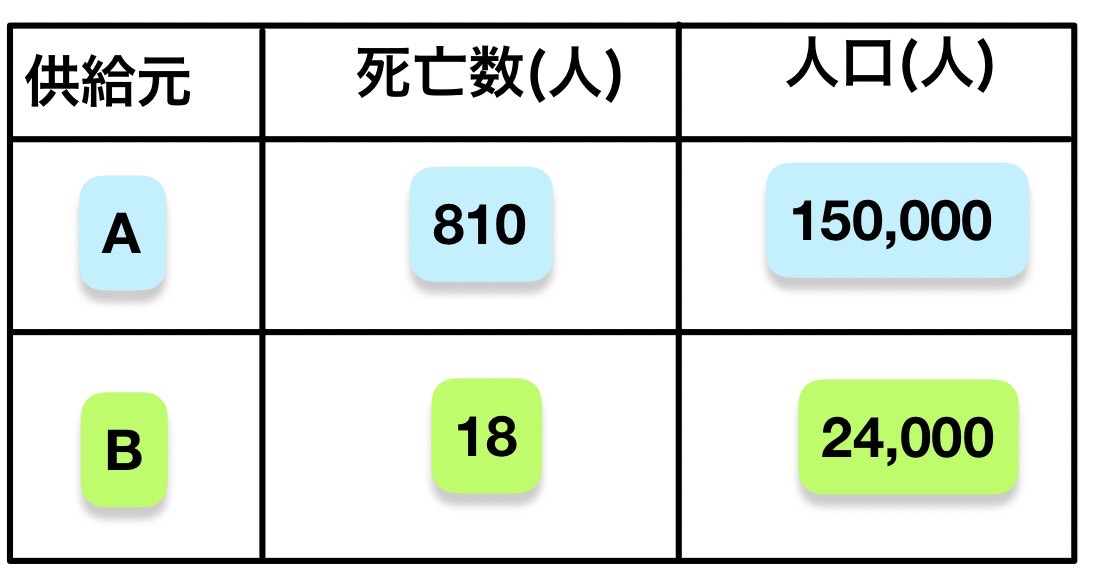
この疾患の死亡に関するAのBに対するリスク比を計算せよ。
ただし、小数第3位以下の数値が得られた場合には、小数第3位を四捨五入すること。
解答:①.②③
死亡に関するAのBに対する相対危険度(リスク比)は、
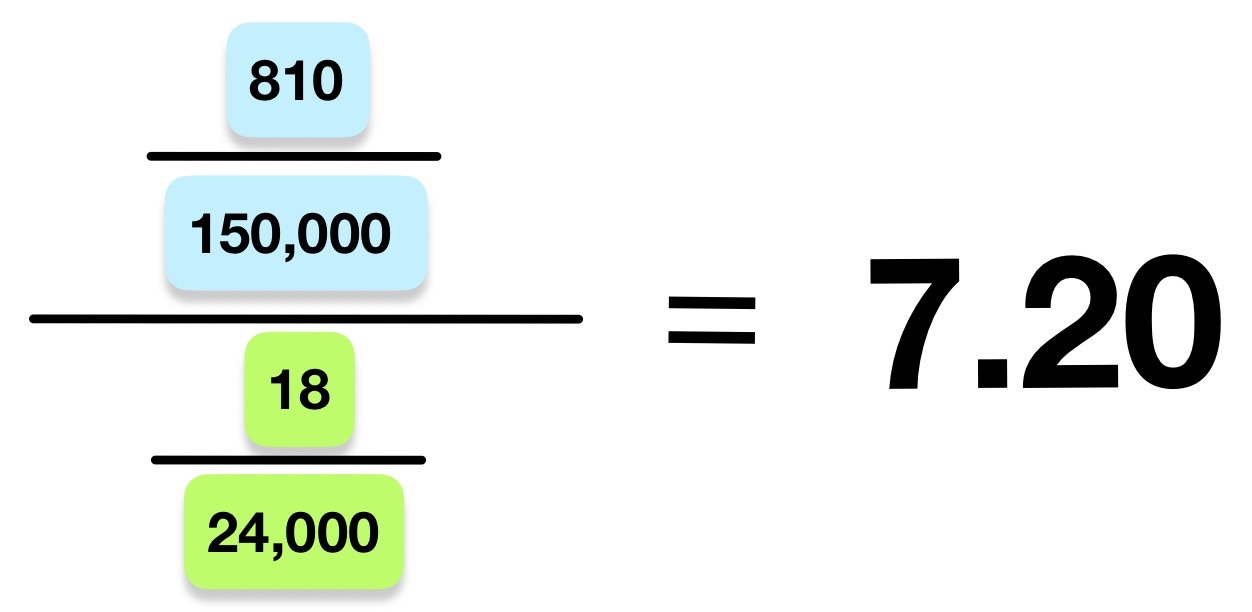
Aから供給される水を飲む人はBから供給される水を飲む人に比べて7.20倍コレラで死亡しやすいということである。
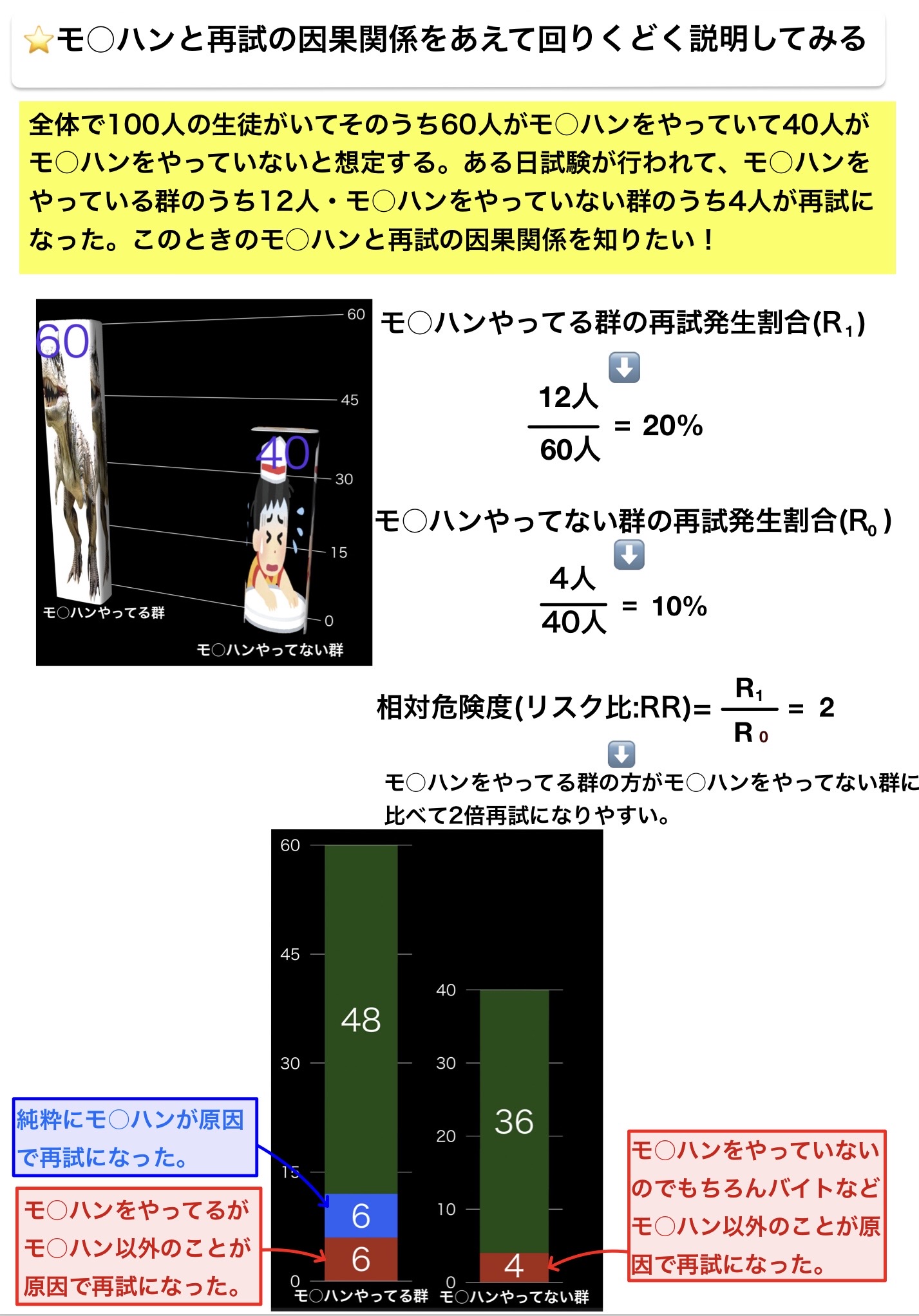
寄与危険度

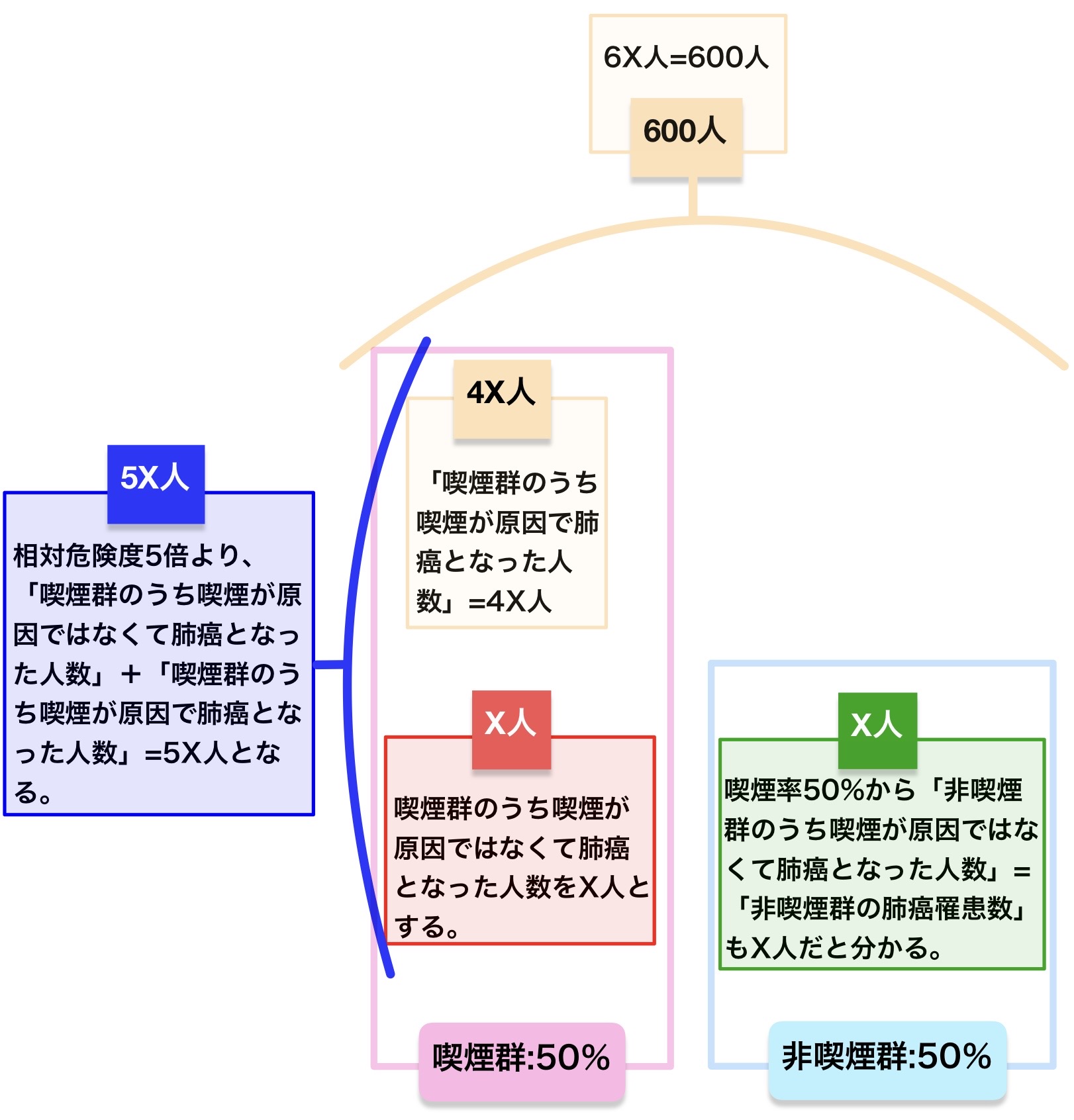
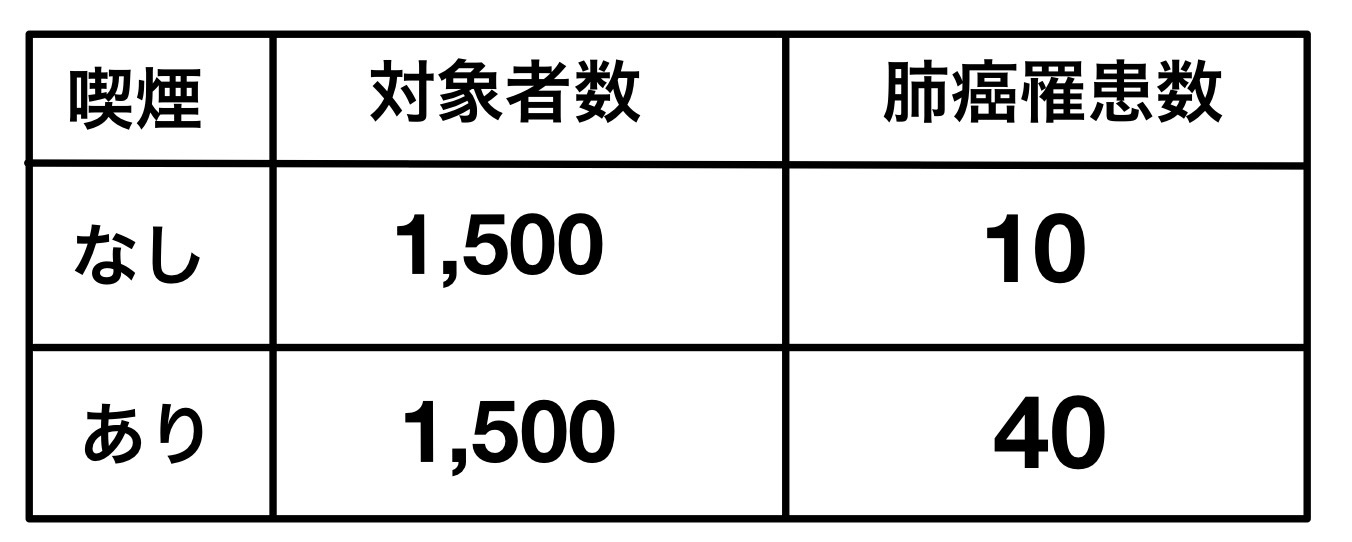
108B40:ある地域における成人男性の肺癌罹患数は1年間に600名である。この地域の成人男性の喫煙率は50%で、喫煙による肺癌罹患の相対危険度は5倍である。
この地域の成人男性において喫煙により増加したと考えられる肺癌の罹患数はどれか。
- 200
- 250
- 300
- 400
- 480
解答:4.400
解説:重要なのは「曝露群のうち曝露が原因ではなくて罹患した人の割合と非曝露群のうち罹患した人の割合は一緒である」ということのみである。
ここら辺の話はこれが根底にある。
これによって全体を考えることなく罹患者に絞って考えることができるのである。
「曝露群のうち曝露が原因ではなくて罹患した人数」=「喫煙群のうち喫煙が原因ではなくて肺癌となった人数」をX人とすると上手く解けるようになっている。
喫煙率50%から「非喫煙群のうち喫煙が原因ではなくて肺癌となった人数」=「非喫煙群の肺癌罹患数」もX人である。
相対危険度5倍より、「喫煙群のうち喫煙が原因ではなくて肺癌となった人数」+「喫煙群のうち喫煙が原因で肺癌となった人数」=5X人となる。
「喫煙群のうち喫煙が原因で肺癌となった人数」=4X人と6X人=600人という情報から答えを出す。
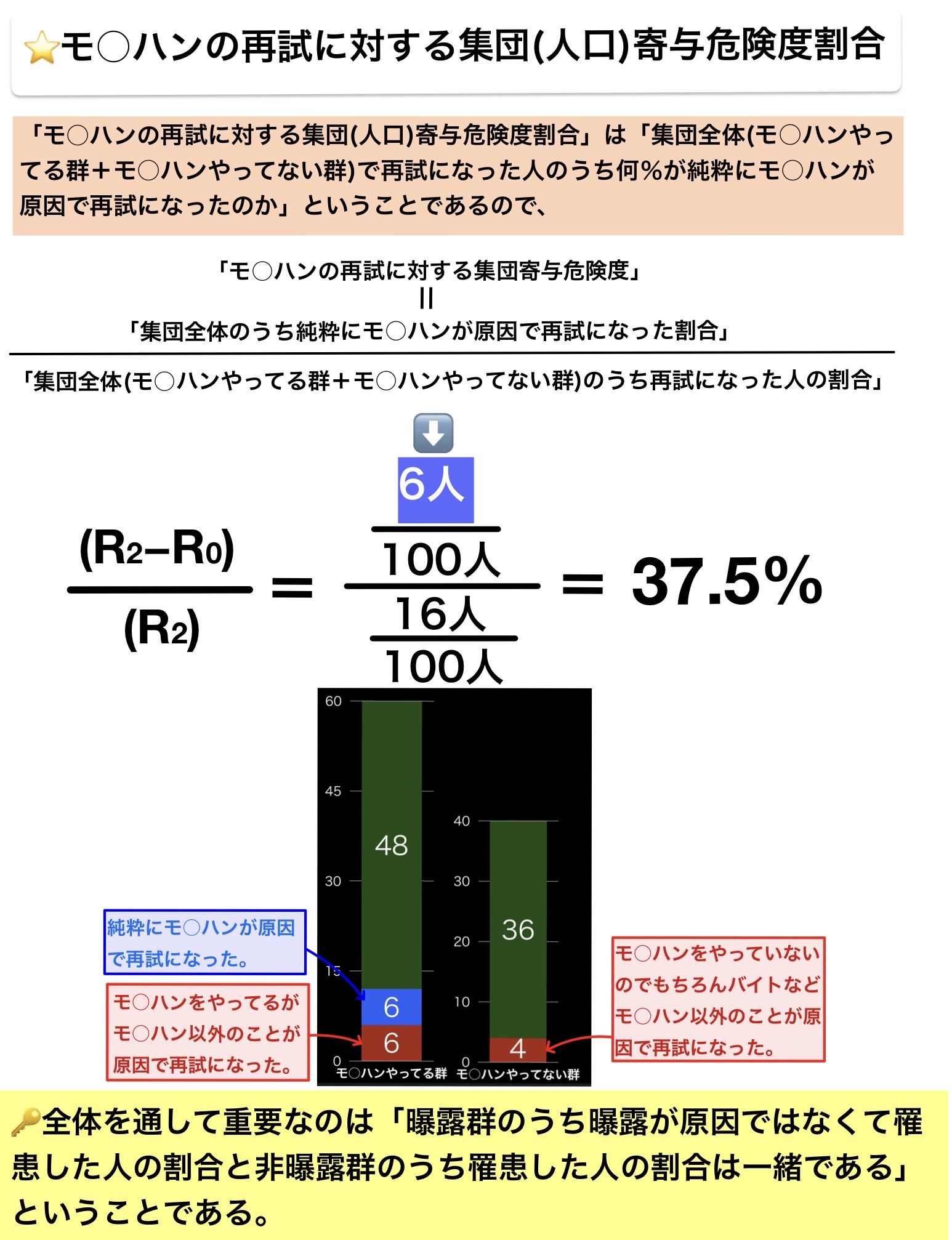
寄与危険度割合

人口寄与危険度(集団寄与危険度)
人口寄与危険度割合(集団寄与危険度割合)
111G69:喫煙の肺癌に対する影響について調べるために、男性地域住民3,000人から構成されるコホート集団を10年間にわたり観察し、表のような結果が得られた。
この集団における喫煙の肺癌に対する人口寄与危険度割合を求めよ。
ただし、小数第3位以下の数値が得られた場合には、小数第3位を四捨五入すること。
解答:0.60
[保健師国家試験問題2011年度午前問題30]
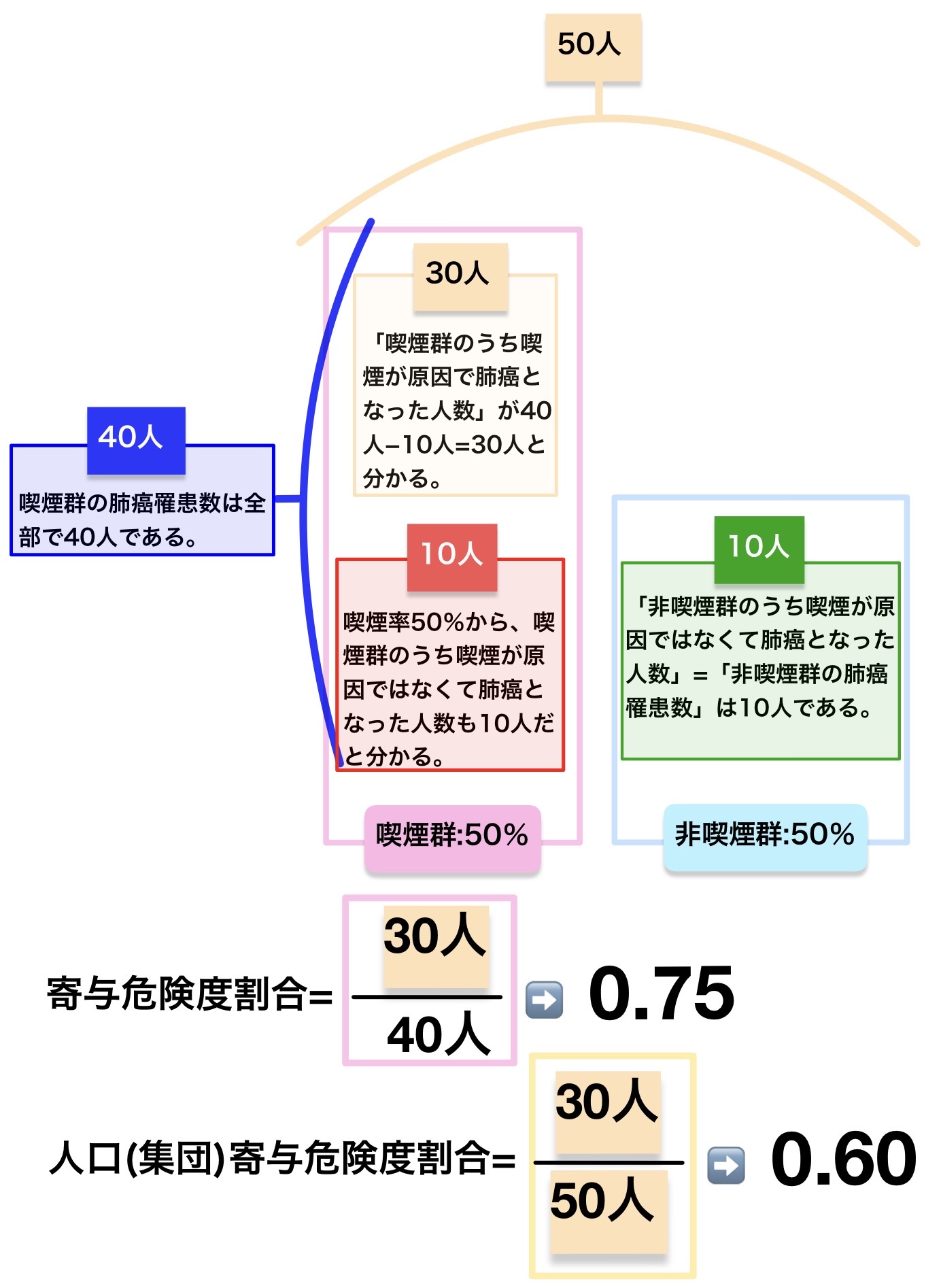
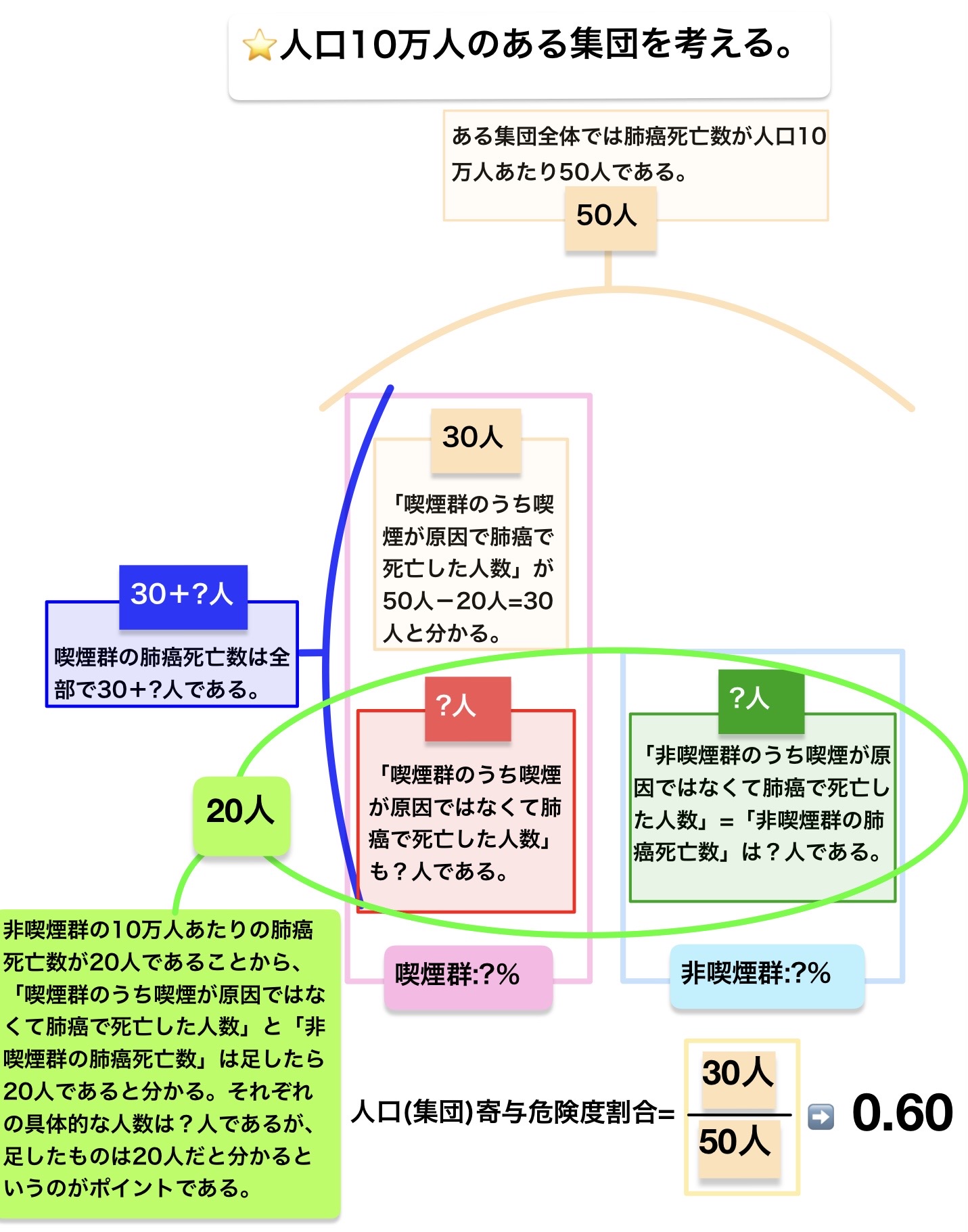
人口 10 万人当たりの年間の肺がん死亡率が、喫煙者では 100、非喫煙者では 20、集団全体では 50 であった。
人口寄与危険割合はどれか。
- 30%
- 40%
- 50%
- 60%
- 80%
解答:4.60%
解説:

「喫煙の肺がん死亡率に対する人口寄与危険度」は「集団全体(喫煙群+非喫煙群)のうち肺がんで死亡した人の割合(R2)=10万人当たり50人から集団全体のうち喫煙以外が原因で肺がんで死亡した人の割合を引いたもの」である。
「集団全体のうち喫煙以外が原因で肺がんで死亡した人の割合」は「非喫煙群のうち喫煙していないのでもちろん喫煙以外のことが原因で肺がんになった割合(R0)=10万人当たり20人」と同じである。
喫煙群のうち肺がんで死亡した人の中には、「純粋に喫煙が原因で肺がんになり死亡した人」と「喫煙していたが喫煙以外のことが原因で肺がんになり死亡した人」がいることに注意する必要がある。
「曝露群のうち曝露が原因ではなくて罹患した人の割合と非曝露群のうち罹患した人の割合は一緒である」ので「喫煙群のうち喫煙が原因ではなくて肺がんになり死亡した人の割合と非喫煙群のうち肺がんになり死亡した人の割合は一緒である。
集団全体が非喫煙群だったら10万人当たり20人しか肺がんで死亡しないはずなのに実際には10万人当たり50人死亡している。10万人当たり30人肺がんで死亡した人が増えているということであり、これは喫煙群のうち純粋に喫煙が原因で肺癌となり死亡した人の影響ということである。
上記のようにこの問題を解くために喫煙者の死亡率は必要ないが、参考のために喫煙者の死亡率を用いてより具体的に全体像を把握してみる。
集団全体を10万人として喫煙群をX万人とすると非喫煙群は(10-X)万人となる。
「集団全体の肺がん死亡率が10万人当たり50人」であり「喫煙群の肺がん死亡率が10万人当たり100人」であり「非喫煙群の肺がん死亡率が10万人当たり20人」であることから以下の式を立てる。

「集団全体が10万人で50人が肺がんで死亡した」とすると、「喫煙群=3.75万人で喫煙群のうち37.5人が肺がんで死亡した」ことになり「非喫煙群=6.25万人で非喫煙群のうち12.5人が肺がんで死亡した」ということになる。
また、「喫煙群のうち3.75万人÷10万人✖️20人=7.5人が喫煙以外のことが原因で肺がんとなり死亡した」ことになり「喫煙群のうち37.5人−7.5人=30人が純粋に喫煙が原因となり肺がんになって死亡した」ことになる。
よって、集団全体で肺がんとなり死亡した人のうち純粋に喫煙が原因となり肺がんになって死亡した人の割合は30人÷50人=0.6=60%である。
総再生産率
合計特殊出生率は「1人の女性が出産可能年齢である15~49歳までに産む子供の数の平均」を示す。
総再生産率は「女児に限定した合計特殊出生率であり、1人の女性が出産可能年齢である15~49歳までに産む女児の数の平均」を示す。純再生産率は総再生産率に死亡率を考慮して導出したものだが、問題を解くときは総再生産率と純再生産率を同義と考えても大きな問題は生じないと思われる。
112F84:ある地域の15歳から49歳までの女性人口と出生数を表のように仮定する。
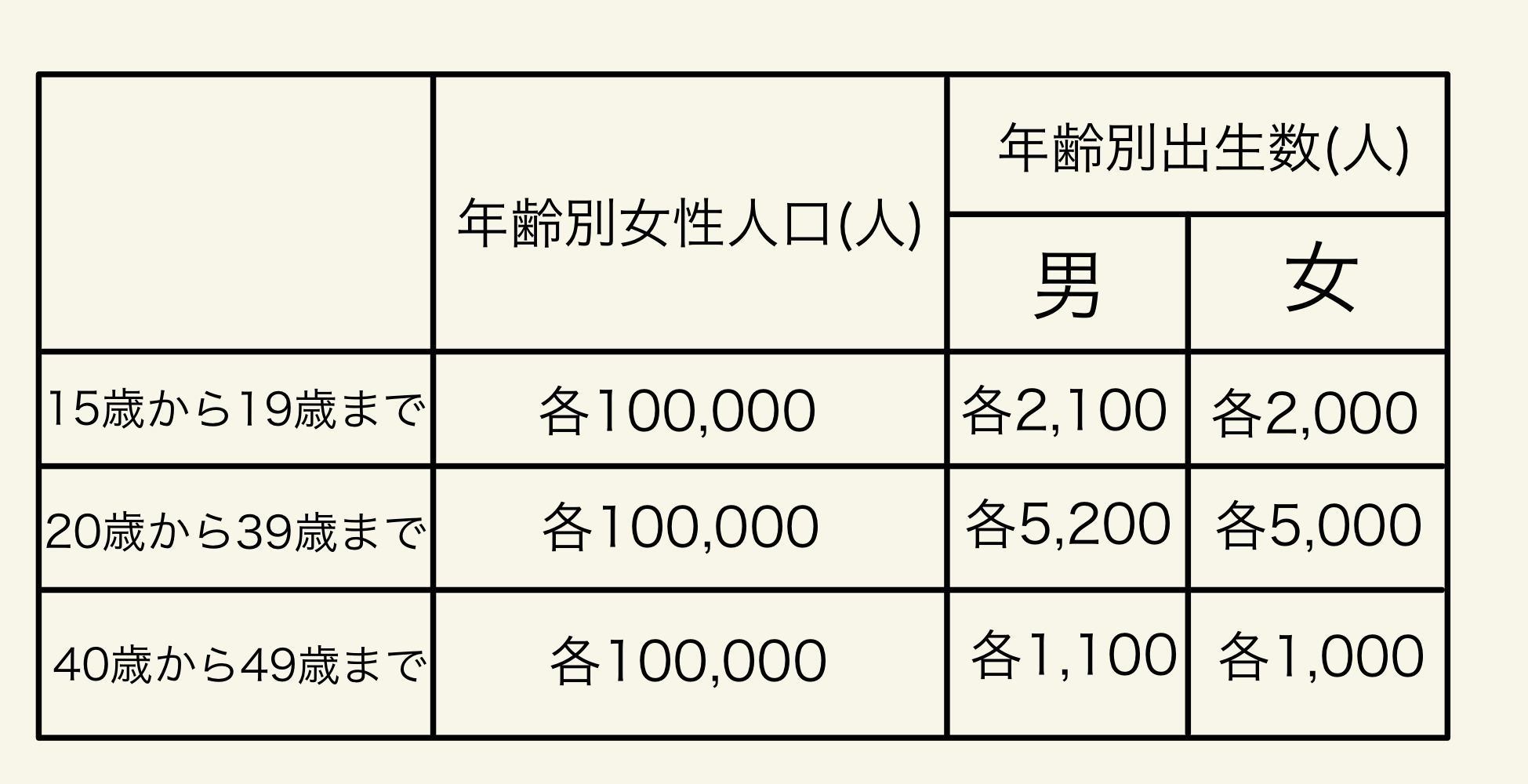
※ 15歳から49歳までの総女性人口 3,500,000人
総再生産率を求めよ。
ただし、小数第2位以下の数値が得られた場合には、小数第2位を四捨五入すること。
解答:①.②

年齢調整死亡率


年齢調整死亡率(直接法)とは観察集団の人口の年齢構成を基準集団の人口の年齢構成に直した場合に求められる死亡率だと考えれば良い。
例えば先進国は高齢者の割合が高いので粗死亡率は高齢者の割合が低い発展途上国に比べてどうしても高くなる。しかし、「先進国の死亡率は発展途上国に比べて高い」という文は違和感がある。そこで年齢調整死亡率(直接法)を用いることで年齢構成の差が死亡率に与える影響を無くそうとするのである。
114C75:人口12万人のA市のある年の死亡者数は510名であった。A市の年齢群別の人口と死亡者数、同じ年の日本全国の年齢群別の人口の概数を示す。
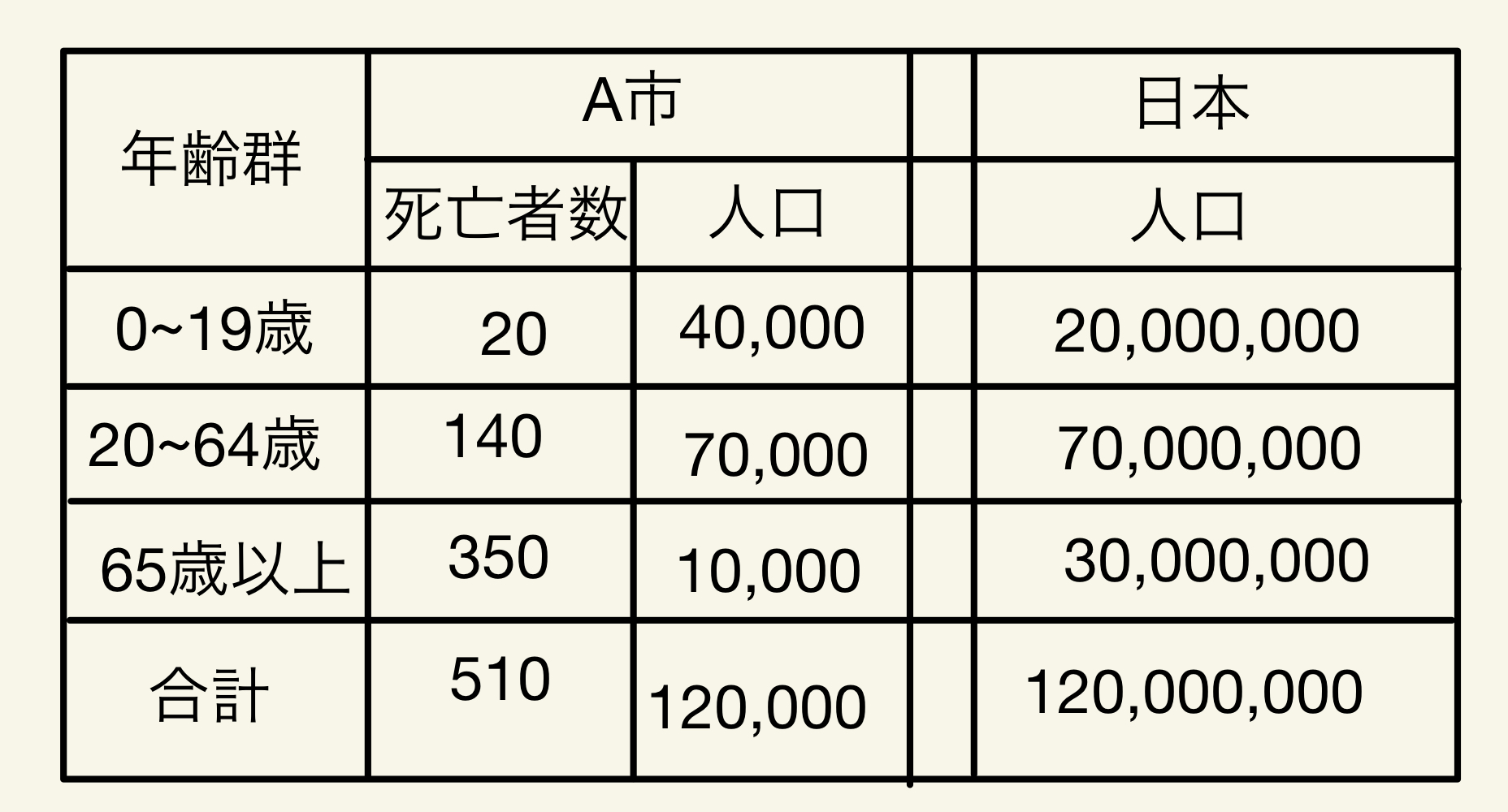
表の日本全国の人口を基準人口としたとき、A市の人口1,000人あたりの年齢群で調整した死亡率を直接法で計算せよ。
ただし、小数第2位以下の数値が得られた場合は、小数第2位を四捨五入すること。
解答:①②.③/人口1,000対
A市の人口の年齢構成が日本全国の人口の年齢構成と一緒だとすると、

このときA市の年齢群別の死亡率は変わらないので死亡者数は、

120000人中1200人が死亡することになるので10.0人/1000対となる。
A市はやたら高齢者が少なく若者が多いので、日本全国の人口の年齢構成にすると死者が増えるということである。
- 2.4%
- 2.8%
- 3.0%
- 3.6%
- 3.8%
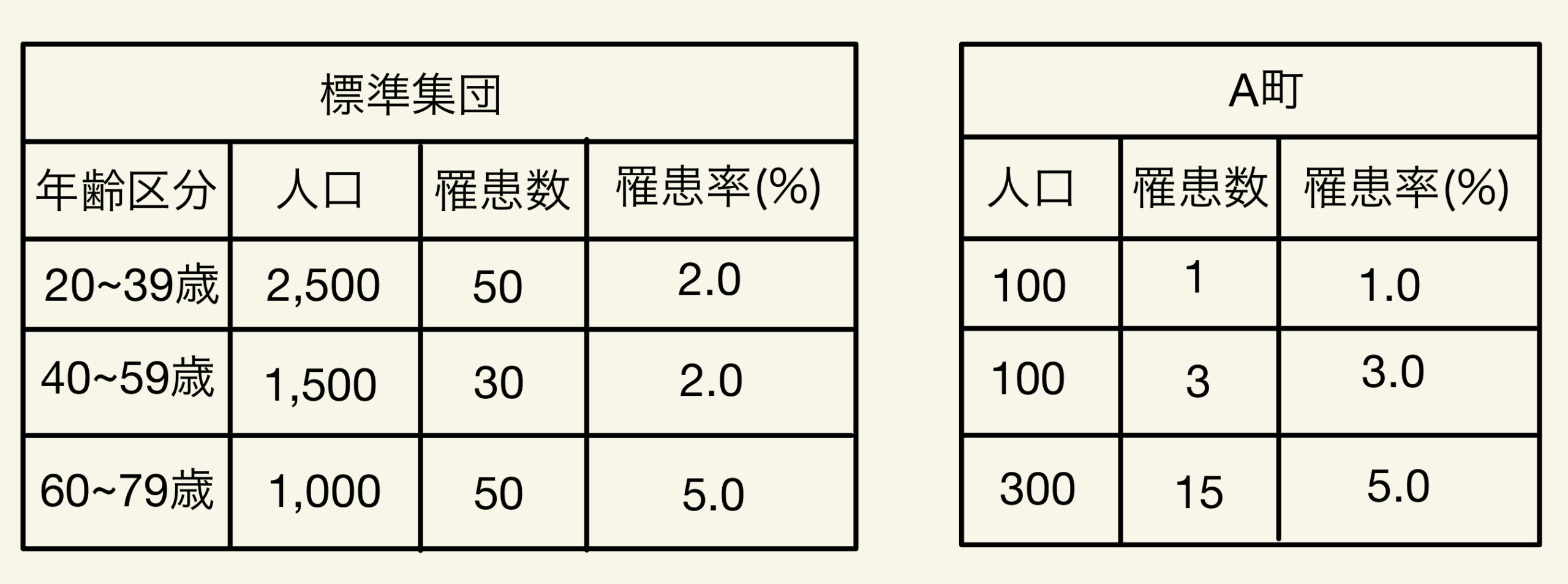
A町の人口の年齢構成が標準集団の人口の年齢構成と一緒だとすると、

このときA市の年齢群別の罹患率は変わらないので罹患数は、

500人中12人が罹患することになるので標準化罹患率は2.4%となる。
標準化死亡比
95A18:昨年1年間のA町(人口10,000人)における全がん死亡数は50であった.昨年の日本全国における全がん死亡率は人口10万対250であった.A町の性・年齢階級別人口と全国の性・年齢階級別全がん死亡率との積和は50であった.
A町の全がん標準化死亡比〈SMR〉はどれか.
- 0.2
- 0.5
- 1
- 2
- 5

解答:3.1
標準化死亡比とは基準集団の年齢階級別死亡率を観察集団に適用して算出する期待死亡数と実際の観察死亡数を比べるものである。直接法と違って、「観察集団の年齢階級別死亡率が分からなくても算出できる」というのが利点である。
109G43:ある工場の作業者において、過去5年間に16名の肝癌による死亡が確認された。死亡数が全国と比較して多いかどうかを知るために標準化死亡比を求めることとなった。
算出に必要な情報の組合せはどれか。
全国データ ———————- この工場の作業者のデータ
- 年齢階級別人口 ————————年齢階級別肝がん死亡率
- 年齢階級別肝がん死亡率 ———— 年齢階級別観察人年数
- 年齢階級別肝がん死亡率 ———— 年齢階級別肝がん死亡率
- 年齢階級別肝がん死亡数 ———— 年齢階級別観察人年数
- 年齢階級別肝がん死亡数 ———— 年齢階級別肝がん死亡率
解答:2.年齢階級別肝がん死亡率 ———— 年齢階級別観察人年数
解説:選択肢2と選択肢3で迷うかもしれないが、標準化死亡比のある意味を考えれば選択肢3ではなくて選択肢2であることが分かる。標準化死亡比は直接法と違って、「観察集団の年齢階級別死亡率が分からなくても算出できる」というのが利点である。
平均余命
110G11:x歳での生存人数をlxとし、x歳以上の定常人口をTxとした場合、x歳の平均余命はどれか。
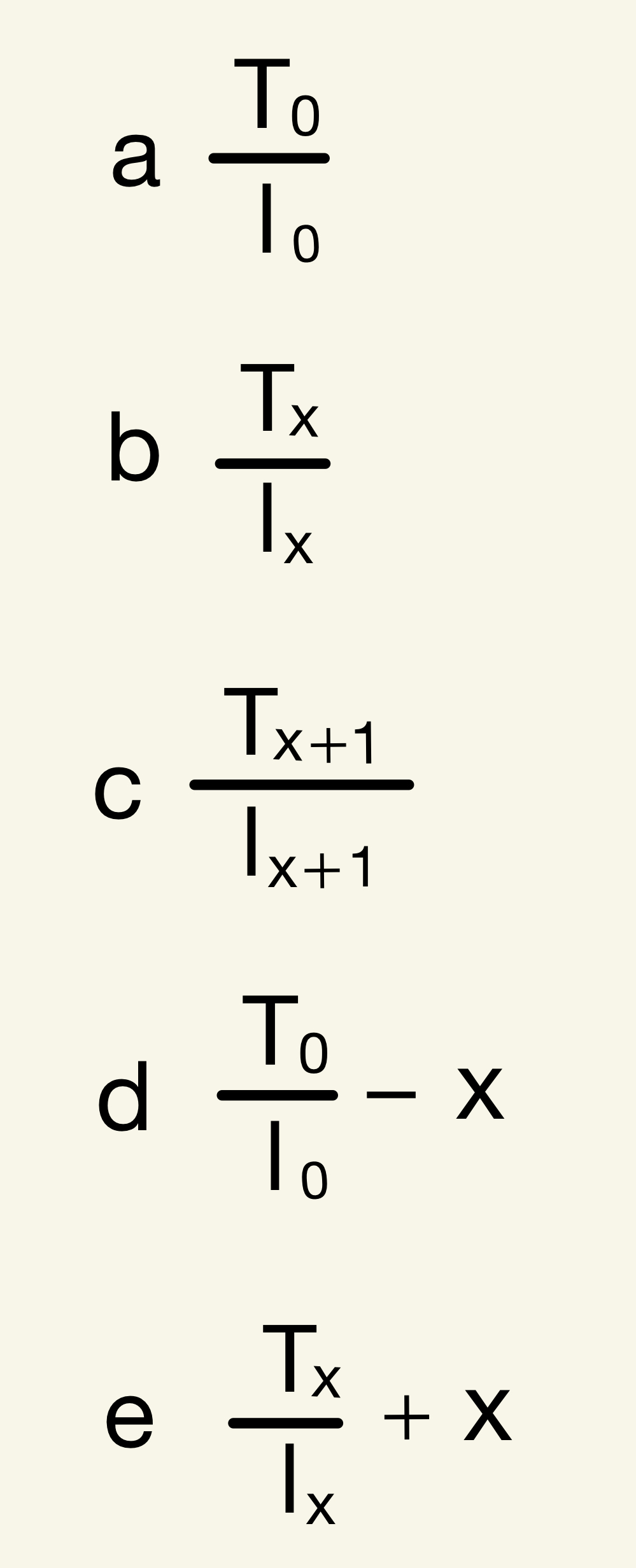
解答:b
解説:
2017年に創設されたある部活の毎年の入部者数を4人としてその部活の定常部員数が12人である場合、平均部活在籍年数は3年である。
ある部活の毎年の入部者数をX人としてその部活の定常部員数が3X人である場合、平均部活在籍年数は3年である。
細かく考えずに「毎年X人入ってきて毎年X人出ていって定常数が保たれる」という大まかなイメージが大切である。
x歳での生存人数をlx=X人としてx歳以上の定常人口をTx=3X人年である場合、平均余命は3年となる。
x歳以上の平均余命はTx÷lxで求められることが分かる。
こういう考え方でも一応解けるというだけであり厳密では全く無い。



コメント